推荐系统:基本件

函数变换

q_adjuster

有时模型预估值分布得较为密集，为了让不同的item更有区分性，方便下游使用，经常用一些函数变换来分布。这里列一些常用的。

一种是拉伸q值较小部分的： \[ q_{adjust} = \frac{q * (1+\text{factor})}{1+\text{factor} * q} \] 其中factor越接近于0，变换后的分布越等价于不变，越大越拉伸q值较小的部分，一般用1.5就差不多了。

norm

类别

1、除以q的均值

• TODO：尝试从data_norm（Instance Normalization）的角度去理解一下

2、batch norm

参考：https://kexue.fm/archives/6992

3、RMS Norm

4、layer norm

5、group layer norm

norm位置

Post-Norm

残差设计作为深度网络的标配，设x的方差是\(\sigma_1^2\)，设F(x)的方差是\(\sigma_2^2\)，并且假设两者互相独立，那么x+F(x)的方差为\(\sigma_1^2 + \sigma_2^2\)，随着层数加深，输出层的方差将呈指数级增长，即残差结构会放大方差。考虑到『当输出数值方差过大时，容易导致在模型中的某一层变成接近onehot而梯度消失』，需要缩小其方差。

最直接的方案是在残差后加Norm，保证每次残差操作后输出层的方差都重新标准化到1上： \[ \begin{align} x_{t+1} &= \text{Norm}(x_t + F_t(x_t)) \\ &= \text{Norm}(\text{Norm}(x_{t-1} + F_{t-1}(x_{t-1})) + F_t(x_t)) \\ &= \text{Norm}(\text{Norm}\textcolor{blue}(\text{Norm}^{...}\textcolor{red}(x_{0} + F_{0}(x_{0})\textcolor{red}) + ... + F_{t-1}(x_{t-1})\textcolor{blue}) + F_t(x_t)) \end{align} \] 但从上式能很明显地看出，恒等分支传到t+1层时，其量级已被指数级缩小（设每一层的标准差都为2，那么传到t+1层时，\(x_0\)已被缩小\(2^{t+1}\)倍），相当于削弱了恒等分支，每Norm一次就削弱一次恒等分支的权重。即Post-Norm的梯度流会更侧重于残差分支。故在较深的网络中，Post-Norm容易导致梯度消失（gradient vanishing），模型难以训好。

当然这是模型参数初始化问题，是一个收敛难易的问题，而非模型拟合能力的问题。若训练后x+F的标准差是小于1的数，那么Norm的操作便会放大恒等分支的权重，所以如果模型能较好地收敛，那也没啥问题。

参考：https://kexue.fm/archives/8620#%E6%AE%8B%E5%B7%AE%E8%BF%9E%E6%8E%A5

Pre-Norm

为保证残差的恒等映射，Pre-Norm采用什么时候用什么时候做Norm的方案，即保证了恒等映射，又避免了方差呈指数级增长（Pre-Norm的方差随模型深度线性增长）： \[ \begin{align} x_{t+1} &= x_t + F_t(\text{Norm}(x_t)) \\ &= x_{t-1} + F_{t-1}(\text{Norm}(x_{t-1})) + F_{t}(\text{Norm}(x_{t})) \\ &= x_{0} + F_{0}(\text{Norm}(x_{0})) + ... + F_{t-1}(\text{Norm}(x_{t-1})) + F_{t}(\text{Norm}(x_{t})) \end{align} \] 但依然会存在问题。因为Norm的存在，后面的各项应该量级相同（若为一个合理的模型， \(F_0、...、F_t\) 这些函数变换应该在相同的量级上），故当 t 较大时，便有（类似于100+1≈100）： \[ \begin{align} x_{t} &= x_{0} + F_{0}(\text{Norm}(x_{0})) + ... + F_{t-2}(\text{Norm}(x_{t-2})) + F_{t-1}(\text{Norm}(x_{t-1})) \\ &\approx x_{0} + F_{0}(\text{Norm}(x_{0})) + ... + F_{t-2}(\text{Norm}(x_{t-2})) \\ &= x_{t-1} \end{align} \] 故： \[ \begin{align} x_{t+1} &= x_{t-1} + F_{t-1}(\text{Norm}(x_{t-1})) + F_{t}(\text{Norm}(x_{t})) \\ &\approx x_{t-1} + F_{t-1}(\text{Norm}(x_{t-1})) + F_{t}(\text{Norm}(x_{t-1})) \end{align} \] 即，当层数较深时，Pre-Norm相当于把模型变宽了，模型的深度没怎么增加。即Pre-Norm的梯度流会更侧重于恒等分支。故在较深的网络中，Pre-Norm容易导致表征坍缩（representation collapse），即深层表示过于相似，额外层的贡献逐渐减弱，从而削弱了模型学习能力。

与Post-Norm不同，Pre-Norm的设置便是模型拟合能力的问题了。

参考：https://kexue.fm/archives/9009

HC

Post-Norm与Pre-Norm两者取其中，几个Pre-Norm后加一个Post-Norm，以此权衡梯度消失与表征坍缩的问题，算是最直接的方案。

这个权衡问题，本质上权衡的是什么呢？Post-Norm与Pre-Norm预设了残差层的输出与输入的连接强度，本质上权衡的就是这个连接强度。

门控机制

element-wise multi

做gate时，用于计算gate的特征一般要先freeze掉：避免互相影响。

gate输出的值，一般都用[-15, 15]截断后过sigmoid再乘个2：正则化&保持输出的期望为1。

feild gate

poso

senet

ppnet、epnet都属于这种。

cgc

attention（transformer）

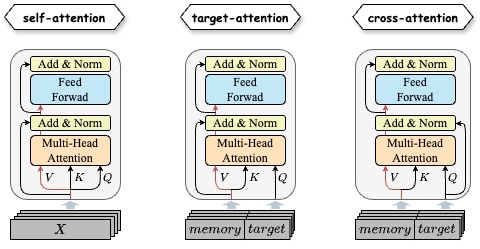
MHA的计算逻辑为： \(\text{softmax}(Q \times K^T + mask) \times V\)

• Q、K、V的形状均为 [batch_size, num_heads, seq_len, head_dim]
• 简略为 \((QK^T)V\) 以便说明：
  • 括弧外为第一部分，即attention的操作，其实就是对V中的向量做各种不同权重的线性组合（V中的行向量为各位置的”原始向量”）；attention_weights的第i行代表的是，计算（输出）第i个位置的表征时，对V中各位置原始向量的线性组合系数（因为softmax的存在，实际上是各位置原始向量的加权平均）。
  • 括弧内为第二部分，即attention_weights（『各种不同权重的线性组合』中的权重，形为 [batch_size, num_heads, seq_len, seq_len]）。一般通过对Q、K选择不同的src，以实现不同效果的注意力机制。
    • 第i行中的权重值 由Q的第i行向量与K中各向量分别做内积得到，即计算（输出）第i个位置的表征时所使用的信息更多的来自于V中哪个位置的向量，需要看Q中第i个位置的向量与K中哪个位置的向量内积更大。
    • 对V的信息提取由Q的维度决定，Q有多少行 便是 提取多少个维度的结果（各维度的含义是什么，由模型结构和数据含义一起合力决定）。
  • 一些不同注意力效果的例子：
    • self-attention中QKV都用输入本身（即target、memory均为同一个src），自注意力的特征提取过程中，每个位置的输出都融合上其它位置的信息，从而捕捉到每个位置间的依赖关系；
    • target-attention中Q用target，KV用memory，代表要从memory中提取target维度的信息，至于要不要有残差结构，各有说法，具体任务具体实验；若有残差结构，target-attention的残差结构用V做为加和项，预期输出的主体是memory，即预期输出的信息是memory的子集；
    • cross-attention中Q用target，KV用memory，与target-attention相同，代表的是从memory中提取target维度的信息，不同的是cross-attention的残差结构用Q做为加和项，预期输出的主体是target，即预期输出的信息是由target生成的，memory的信息在该生成过程中扮演context或condition的角色（当然能否达到该效果，也由训练数据含义/分布决定）；
    • 为了保证QK^T的结果作用到V上时具有attention_weight的能力，K、V的src一般需要用同一个，故通过对Q、K选择不同的src以实现不同注意力效果的例子，除上述三种外，还有一种便枚举完所有合理的可能了（这最后一种暂未想到具体的任务场景，待后续再补充）：Q用memory，KV用target，残差结构用V或者Q做为加和项，其实这种结构就是target-attention和cross-attention，只不过数据输入时将target和memory对调了下，是否存在物理含义待定。

几种掩码：

• full visible：常见于encoder。
• causal：常见于decoder。
• 对角线：常见于单点训练的并行化。

一些技巧：

• 因残差结构的设计，若想计算对序列信息的汇总又想把MHA的建模能力用上，可以增加一个槽位，并塞一个任一不随样本变化的token（比如CLS），计算该位置的输出时不做任何mask即为所有序列信息的汇总（具体汇总含义，由label定义）。
• 分析时，看attention_weights的均值、方差以及直方图分布。比如如果发现所有权重的均值都差不多，说明attention压根就没起作用，要么是序列特征出问题了，要么是target_item构造的emb有问题。

hstu

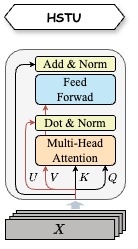
hstu的计算逻辑为： \(\text{FFN} \textcolor{red}(((\text{sigmoid}(Q \times K^T+bias) \odot mask) \times V) \odot (mask \times U)\textcolor{red}) + X\)

• Q、K、V的形状均为 [batch_size, num_heads, seq_len, head_dim]，经过mask后的U的形状为 [batch_size, seq_len, num_heads*head_dim]
• 对该结构有几种不同的理解
  • 视角1：本质上是resnet版的senet在序列特征上的适配。通过MTA产出各位置的权重，对（经过线性变换后的）原向量U做reweight；即让V去学特征重要度，但因为V只有当前位置的视角，建模能力有限，故通过QK的attention_weight实现更个性化的带权pooling。
  • 视角2（后续思考可以该视角为主）：高低阶特征交叉，DCN在序列特征上的适配。类似DCNv2的逻辑（用『左乘一个行向量（线性加权组合）的结果与要交叉的特征做哈达玛积 \(x_0 \odot (w^T x_0) + x_0\) 』来等价『与要交叉的特征做外积后的结果 内积一个列向量 \((x_0 x_0^T) w + x_0\) 』的操作），MHA完成线性加权组合的操作，与（经过线性变换后的）原向量U做哈达玛积，实现序列特征的隐式交叉。
• 使用时，若只基于该结构（类似于GR中的encoder-only结构），用用户的历史序列预测target(item)的action，user和item的交叉不够显式，只有隐式地将其它位置的信息线性加权到item上来，可能难以训好。

token-mixer

ID系统

离散ID

语义ID

向量量化变分自动编码器(VQ-VAE)

残差量化变分自动编码器RQ-VAE

局部敏感哈希(LSH)