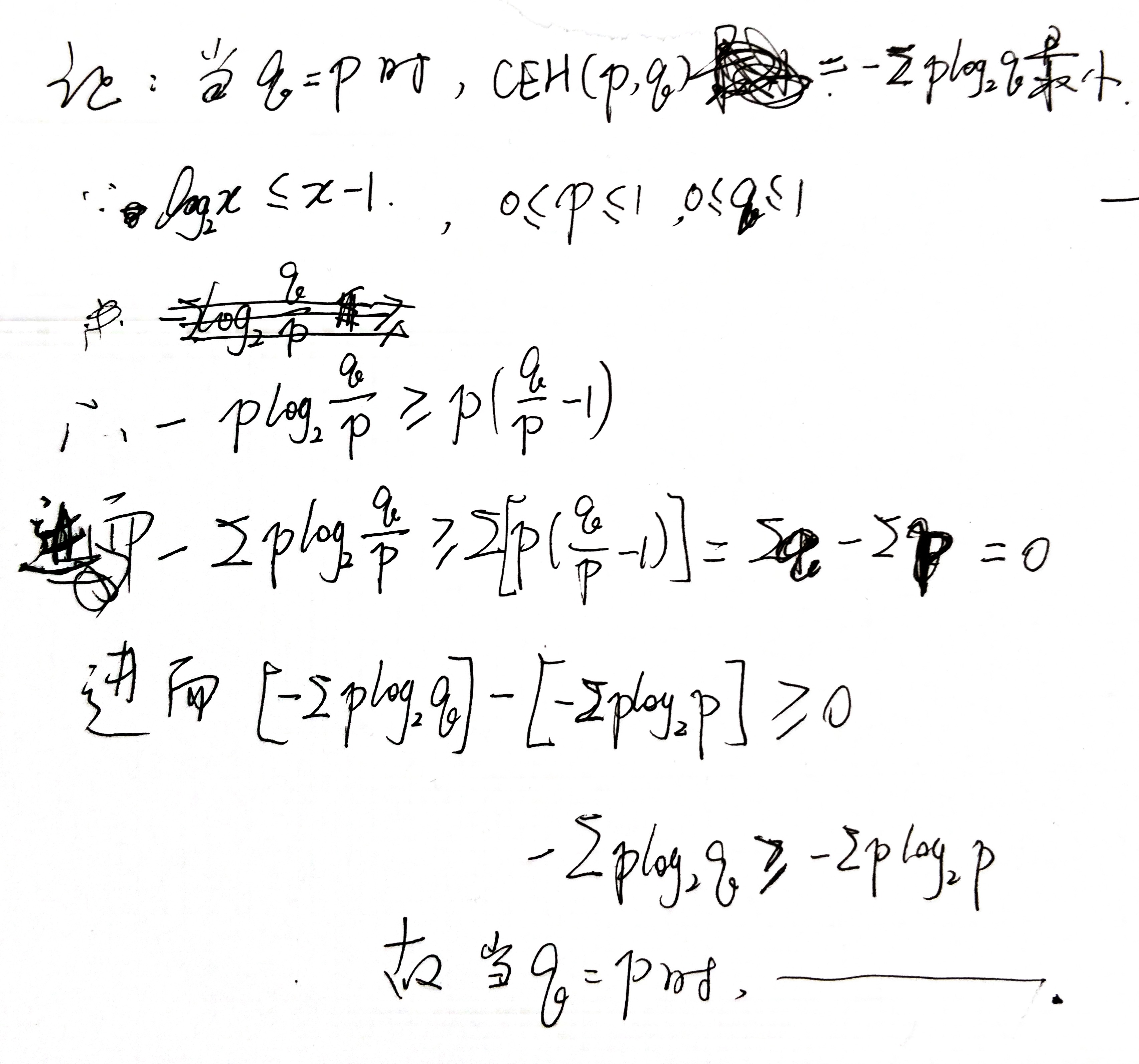
熵可以认为是随机变量的数字特征,其含义为为确定某一随机变量所需信息量的平均。
设$ X p(x)$ ,则 \(H(X) = H(p) = -\sum p(x) \log_2 p(x)\) ,单位为比特。
若设 \(Y = -\log_2 p(X)\) ,则\(H(X)=E(Y)\) ,即随机变量的熵为随机变量函数的期望。$ -_2 p(X)$ 意为为确定随机变量 \(X\) 的值所需的信息量,(随机变量X的熵是为确定X的值所需要的信息量的期望)若\(p(x)\) 越小,则所需信息量越大。
综上,熵\(H(X)\) 是 \(X\) 信息量的期望。
注:\(X\) 指随机变量,\(x\) 指随机变量取的值。
方差衡量某一变量概率分布的散度( \(X - E(X)\) ),方差越小偏差越小,置信度越高。
熵衡量某一变量概率分布的不确定性( \(-\log (P(X))\) ),熵越小不确定性越小,置信度越高。
衡量两个分布的差异(f为X的真实分布,g为X的估计分布)用相对熵,又称 KL(Kullback-Leibler) 散度: \[ D(f||g) = \sum_{x \epsilon X} f(x) \log \frac{f(x)}{g(x)} \\ = \sum_{x \epsilon X}(- f(x) \log g(x)) - H(X) \] 因为数据集定了后,\(H(X)\) 自然就成了常数,而剩余的一项因其形式,称之为交叉熵,记为 \(CEH(f, g)\) ,为方便计算,在比较大小时,常用交叉熵代替 KL 散度。
设 g 为估计分布,f 为由样本中统计出的分布,N 为总样本数,由最大似然估计可得其似然函数为 \[ \prod g(x)^{Nf(x)}, \] 取对数得: \[ \log \prod g(x)^{Nf(x)} \\ = \sum \log g(x)^{Nf(x)} \\ = N \sum f(x) \log g(x) \] 故最小化交叉熵等价于最大化最大似然函数。
对分布 f 编码所需的最小信息量为 \(CEH(f,f)\) ,而 \(CEH(f,g)\) 均比该值大,称为不完美编码,其中 \(g \ne f\) 。
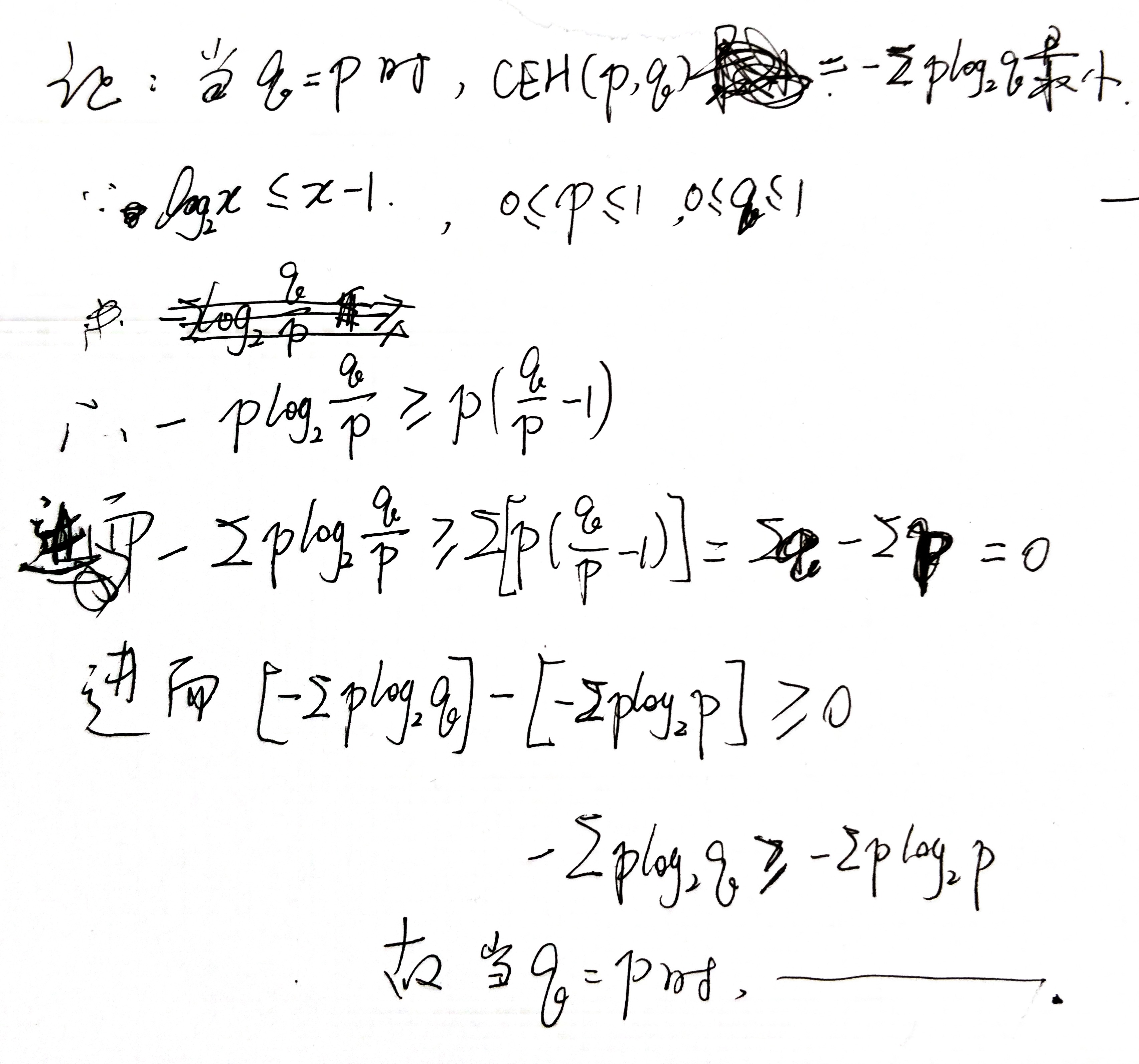
为解决贝特朗悖论出现的问题,作以下三点假设(概率论公理):
\(\xi\) 的数学期望可理解为在 \(\Omega\) 上的加权和(权重为概率值,对应于常规均值中某数出现的频率,有的资料称之为概率平均),采用的计算方法为L-S积分:如设\(\xi=\sum_{i=1}^na_i \chi_{A_i}\) ,即将事件\(A_i\) 映射为实数\(a_i\) ,则\(E(\xi)=\int_{\Omega} \xi(\omega) \mathrm{d}p(\omega)=\sum_{i=1}^n \int_{\Omega} a_i \chi_{A_i} \mathrm{d}p(\omega)\) ,即将\(\Omega\) 中不可分事件\(\omega\) 按值域划分为n类(每一类中的\(p(\omega)\) 都相等,假设\(A_1\) 中有10个\(\omega\) ,则\(p(A_1)=10*\mathrm{d}p(\omega)\) ),并在每一类中积分出一个值,最后将这n个值求和。当n为有限值,结果为\(\sum_{i=1}^n a_i p(A_i)\) ;当\(n\to \inf\) ,结果为\(\int_{-\inf}^{+\inf} a f(a)\mathrm{d}a\) 。
综上,将数学期望作\(\xi\) 在\(\Omega\) 上的“加权和”看待。
- \(E(\xi)\) :
- \(=E(\xi \chi_{\Omega})\) :在\(\Omega\) 上\(\xi\) 的加权和
- \(=E(\xi | \Omega)\) :在\(\Omega\) 上\(\xi\) 的加权平均
- \(E(\xi \chi_A)\) :在\(A\) 上\(\xi\) 的加权和(实质为在\(\Omega\) 上\(\xi \chi_{A}\) 的加权平均,为方便思考,如此定义其含义)
- \(E(\xi | A)\) :\(\xi\) 在\(A\) 上的加权和,然后在\(A\) 上取平均,等于\(\frac{E(\xi \chi_A)}{P(A)}\)
- \(P(A)\) :\(\chi_A\) 在\(\Omega\) 上的加权和
- \(P(A | B)\) :\(\chi_A\) 在\(B\) 上的加权平均
总结:
- \(P(AB)=E( \chi_A \chi_B)\) :单纯地在\(A\) 、\(B\) 交集上的加权和(也可认为在\(\Omega\) 上做的归一化)
- \(P(A|B)=E(\chi_A |B)\) :对在\(A\) 、\(B\) 交集上的加权和还做了归一化,谁为条件便是在哪个集上做的归一化(A、B独立的情况暂不考虑)
- 归一化:在哪个集上做归一化便是将全集缩减为了那个集
\[ \sum_{i=1}^n E(\xi \chi_{B_i}) = E(\xi \chi_B) \\ \Rightarrow \sum_{i=1}^n P(B_i)E(\xi | B_i) = P(B)E(\xi | B) \]
将条件期望乘上条件的概率,可看做是将这个区域上的均值取消求平均的操作
\[ E(\chi_A)=\sum_{i=1}^n E(\chi_A \chi_{B_i}) \\ \Rightarrow P(A) = \sum_{i=i}^n P(A | B_i) P(B_i) \]
\[ P(B_i | A) = \frac{E(\chi_{B_i} \chi_A)}{P(A)} = \frac{P(A|B_i)P(B_i)}{P(A)} \]
\[ P(|x-\mu|\ge \epsilon) \le \frac{\sigma^2}{\epsilon} \]
其中 \(\epsilon\) 为任意正数。该不等式给出了随机变量 x 在分布未知的情况下,事件 \(\{|x-\mu| \le \epsilon\}\) 的下限估计;如 \(P(|x-\mu| < 3\sigma) \ge 0.8889\) 。
数学中似然函数 = \(\prod_ip_i\)(其中 \(p_i\) 为样本\(x_i\) 的概率,一般能用一个含待估计的参数和 \(x_i\) 表示的解析式表示)表示已出现的样本出现的概率,而已出现的样本通常为最可能出现的,故可通过最大化该似然函数来估计想要的参数。有时会对似然函数取对数以简化运算。
在机器学习中常用最大化以假设函数\(h\) 为参数的似然函数的方法使得假设函数\(h\) 逼近隐藏模式\(f\) 。
从物理意义上来去记一些矩阵乘积,一方面可以加快公式推导,另一方面可以对一些公式有更深入的理解。
把线性空间的一个元素(向量、矩阵、……)与一个非负实数相联系,在许多场合下,这个非负实数可以作为向量或者矩阵大小的一种度量,这个非负实数便称为范数(当说长度时,特指的是内积空间中向量的2-范数)。元素与实数的映射关系需满足4点才能称为范数:非负性、定性、齐次性和三角不等式。
范数分类:p-范数、加权范数(\(||x||_A=\sqrt{x^TAx}\))、F-范数(\(\sqrt{\mathrm{tr}(A^TA)}\))、……
- \(L(x_1,x_2)\)意为向量\(x_1\)与\(x_2\)张成的空间;
- \(R(A)\) 意为矩阵\(A\)的列向量张成的空间,称为\(A\)的列空间或\(A\)的值域;
- \(R(A)^{\bot}\)意为 \(A\)的列空间的正交补空间;
- \(N(A)\)意为\(A\)的零空间或\(A\)的核空间。
\(A\)的零空间是\(A^T\)的列空间的正交补空间,而\(A^T\)的列空间维度与A的列空间维度在数量上相等,故\(\mathrm{dim}N(A)=\mathrm{dim}R(A^T)^{\bot}=\mathrm{dim}R(A)^{\bot}=n-rank(A)\),为简化书写与推导,常一步写为\(\mathrm{dim}N(A)=n-rank(A)\)。
一种几何上的解释:\(\mathrm{abs}|A|\) 意为矩阵\(A\)的行向量限制性地张成的空间的体积。(限制性地张成,是指用于线性组合的系数在(0,1)间取值。)
n个变量的二次多项式(每一项的次数都为2的多项式)称为二次型。矩阵形式的二次型为一标量\(x^TAx\),其中\(A\)称为二次型矩阵,虽然无论\(A\)是否对称,\(x^TAx\)总是一个二次型,但A的表现形式(是否对称)并不影响这个标量的结果,即任一非对称阵的形式均有一个对称阵的A与之对应且标量结果相同,故若无特殊说明,默认二次型矩阵为一对称阵。
默认特征向量特指单位化的特征向量(虽然因为有正负还是不唯一,但已足够)。
对称阵的特征值均为实数,特征向量两两正交。
若对称阵的特征值均为正数则必正定(由对称阵必能正交对角化推得),依此类推。
针对最优化问题 \[ \mathrm{min}x^TAx \quad s.t. ||x||_2^2=1 \] 结果为\(A\)的最小特征值,\(x\)为其对应的特征向量。因为\(A\)为对称阵,故能正交对角化\(A=U\Lambda U^T\),原问题便转化为了:将原默认基换为\(U\)的列向量构成的基,于是\(x\)便成为了\(y\),满足\(y=U^{-1}x\) (其过程为\(x\)向\(U\)的各个列向量方向投影,并依列向量次序组织成为\(y\)),因为\(U\)为正交阵,故\(||y||_2^2=1\)依然成立,与此同时,优化目标变为\(\mathrm{min}y^T\Lambda y\),可看做(问题本质并非这样,但脱离问题只就该式子的数学形式来看可如此看待;这种办法只可用于求解不能用于理解)求单位向量\(y\)的方向使其在度量矩阵\(\Lambda\)下长度最小,故结果为\(A\)的最小特征值,而\(x=Uy=y\) ,即只取最小特征值对应的特征向量。
对此常用结果可记住:要使一单位向量在某一度量阵下的内积最小,须使该单位向量等于该度量阵最小特征值对应的特征向量,此时内积便为该度量阵的最小特征值。
在线性空间(对加法和数乘封闭的集合)中,借助于基的概念,线性空间中的元素(矩阵、多项式、函数等)的运算能够转化为向量的运算,线性变换(满足\(T(kx_1 + lx_2) = kT(x_1) + lT(x_2)\)的\(T()\)称为线性变换)的运算能够化为方阵的运算,从而一般线性空间中的问题都能够转化为列向量空间中的问题。故可认为线性代数主要研究列向量空间。
基 A 下的向量 Ax,称 x 为坐标向量,Ax 为向量。在计算时默认用坐标向量,以做线性变换 P 为例进行说明:
其中,\(C=A^{-1}B\)称为过渡矩阵,亦可看做新基在旧基下的坐标;
通法:
通过对在换基\(A \rightarrow B\)前后的同一向量\(Ax\)做相同的线性变换\(P\)可以看出:
线性空间中已有加减,而数乘算不上线性空间内的积,故引入内积的概念,其作用是度量夹角、长度,直觉上可以将 (x, y) 看做 x 在 y 上的投影与 y 长度的乘积。
任何内积空间均应满足不等式\((x,y) \le |x||y|\) 。
因为向量的长度是不应变的,故内积的定义不应依赖于基,由此在定义内积时应用向量而非坐标向量。
比如在线性空间中定义 \((x,y)=x^TGy=\sum_i \sum_j g_{i,j} x_i y_j\) ,其中 G 可以看作是在不同维度上的度量尺,至于具体工作细节可从该式看出:取过渡矩阵 Y,满足\((Y^{-1})^T(Y^{-1})=G\) ,则 \((x, y)= x^T (Y^{-1})^T(Y^{-1})y = (Y^{-1}x)^T(Y^{-1}y)\) ,从而实现度量尺的功能。因为计算时采用坐标向量的习惯,使得度量尺在不同基下的矩阵表示不同,称之为度量阵。
同一度量尺在不同基下的表示称为合同(同一线性变换在不同基下的表示称为相似)。
若 \(L \oplus M=R^n\) ,则将 \(x \epsilon R^n\) 沿着 M 到 L 的投影变换在\(R^n\) 的基下的矩阵称为投影矩阵,记为\(P_{L,M}\) ,且\(P_{L,M} = (X,0)(X,Y)^{-1}\) 。
投影的本质:所谓投影便是依投影面 L 重新建立坐标系,并只保留投影面上的坐标,其余坐标置零。故私以为更准确的词应该叫截取,截取矩阵。
当 M 为 L 的正交补空间时,即\(X^T Y = 0\) ,称其为正交投影: \[ P_L=(X,0)(X,Y)^{-1} = X(X^T X)^{-1}X^T = XX^+ \quad (前提:X列满秩) \] 在统计学中又称\(P_L\) 为 hat matrix,记为 H:
对矩阵求导时按标量求导原则,并遵循以下两条规则:
\[ || X || _2^2 = \sum_{i=1}^N \sum_{j=1}^N x_i^Tx_j = X^TX \]
集合\(C\) 内任意两点间的线段上的点仍在该集合内,则称该集合为凸集。表示为\(\theta x+(1-\theta)y \in C, \theta \in (0,1)\) ,其中\(\theta x+(1-\theta)y\) 称为点\(x\) 与\(y\) 的凸组合。
本质为找函数的零点,用在最优化上便是找函数导数的零点。
\[ w_{t+1} = w_t - (\frac{\partial ^2 L}{\partial w \partial w^T})^{-1} \frac{\partial L}{\partial w}|_{w=w_t} \]
牛顿法相比起梯度往往法收敛速度更快,特别是迭代值距离收敛值比较近的时候,每次迭代都能使误差变成原来的平方,但是在高维时矩阵的逆计算(奇异值分解求伪逆以保证数值稳定)会非常耗时,N * N的矩阵求逆的时间复杂度为\(\mathcal{O}(N^3)\)。
通过引入拉格朗日乘子,可将有 d 个变量与 k 个约束条件的最优化问题转化为 d+k 个变量的无约束优化问题。
\[ \min_x f(x), \\ s.t. \quad g(x)=0. \]
设 x 为 d 维向量,则约束曲面 \(g(x)=0\)是 d-1 维曲面,目标函数\(f(x)\)是 d 维曲面。
\[ \nabla f(x) + \lambda \nabla g(x) = 0, \] 由此得到等价的无约束最优化问题: \[ \min_{x, \lambda} f(x)+ \lambda g(x). \quad (\lambda \neq 0) \]
\[ \min_x f(x), \\ s.t. \quad g(x) \le b. \]
对于不等式约束分两种情况讨论:
将分类讨论的问题合为一个式子,如下(记 g(x)-b=h(x) ): \[ \min_x \max_{\lambda} f(x)+ \lambda h(x), \quad \lambda \ge 0 \] 称上式为原不等式约束最优化问题的等价问题,等价的原因为:
由此,原不等式约束最优化问题可转化为如下不等式约束的拉格朗日函数的最优化问题: \[ \min_x f(x)+ \lambda h(x) \\ s.t. \quad h(x) \le 0 \\ \quad \quad \lambda \ge 0 \\ \quad \quad \lambda h(x) = 0 \] 称以上三个约束条件为KKT(Karush-Kuhn-Tucker)条件。
为使用拉格朗日函数,须将等价问题做如下变型:
对于等价问题(\(\lambda \ge 0\)省略不写,并记\(L(x, \lambda)= f(x)+ \lambda h(x)\)),因为 \[ \min_x \max_{\lambda} L(x, \lambda) \ge \min_x L(x, \lambda) \] 所以 \[ \min_x \max_{\lambda} L(x, \lambda) \ge \max_{\lambda} \min_x L(x, \lambda) \] 称$ L(x, )\(为拉格朗日函数,称\)\(为对偶变量,称\)x L(x, )\(为拉格朗日对偶函数,称等价问题为强对偶问题,称\){} _x L(x, )$为弱对偶问题,称原不等式约束最优化问题为主问题。
强对偶问题与弱对偶问题统称为对偶问题,无论主问题凸性如何,对偶问题始终是凸优化问题。一般弱对偶问题不等价于强对偶问题,但当主问题为凸优化问题,且可行域中至少有一点使不等式约束严格成立,那么弱对偶问题便可等价于强对偶问题,这称为强对偶性。
当强对偶性成立后,直接求解弱对偶问题便可得到主问题的解,具体为:通过拉格朗日乘子法可将不等式约束的最优化问题转为满足 KKT 条件的拉格朗日对偶函数,通过将拉格朗日函数对原变量和对偶变量的导数置零,并结合KKT条件便得到弱对偶问题的解,由强对偶性进而得主问题的解。