机器学习:三个层次

极大似然估计

理解

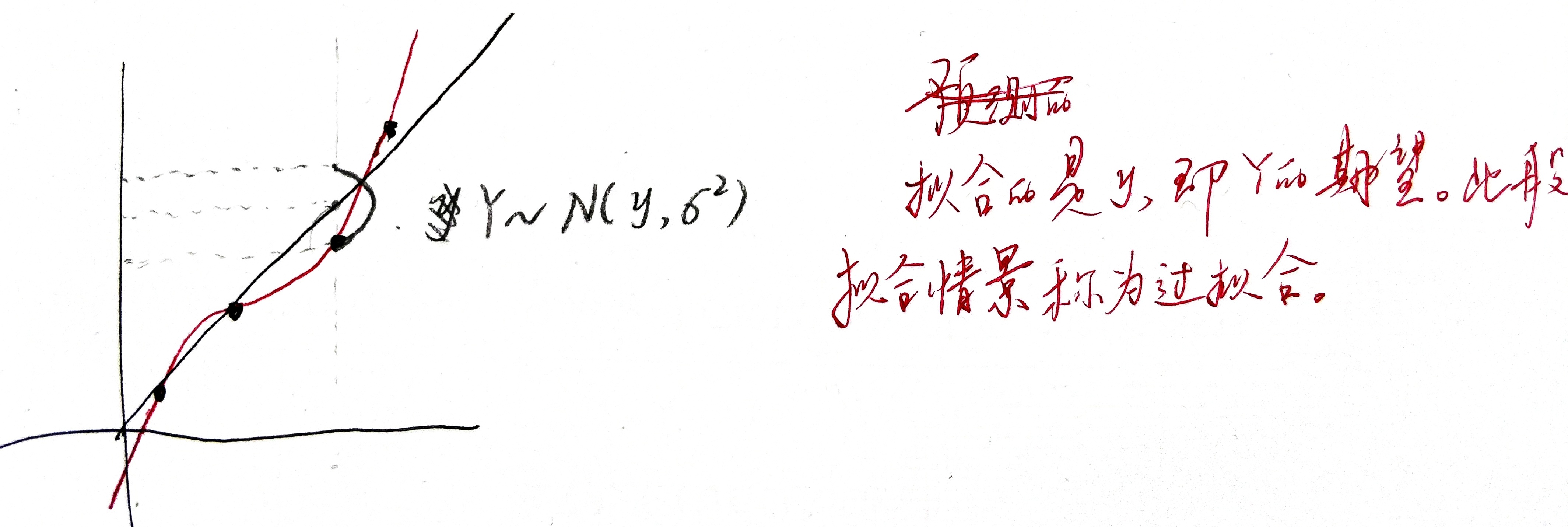
用最大似然来学习数据中的模式时，当数据点数远小于参数数量时，会出现过拟合（因自由度远高于数据点数而导致的某些项被过度调参的情况，当出现这种情况时会导致模型的泛化能力急剧下降）的问题，所以不得不根据可得到的训练集的规模限制参数的数量。这种由表象得出的问题及其解决方案，很明显无法说明最大似然与过拟合的关联性，所以解决方案也显得非常不合逻辑（更为合理的解决方法似乎应是根据待解决问题的复杂性来限制参数的数量），下面以一个例子来说明最大似然与过拟合的内在联系：

假设要估计的 $Y\sim N(\mu ,{\sigma }^2)$ ，暂且不考虑 y 与 x 的关系，当 $\mu$ 已知， $\frac{1}{n}\sum (Y_i-\mu {)}^2$ 是 $\mu$ 的一个无偏估计；

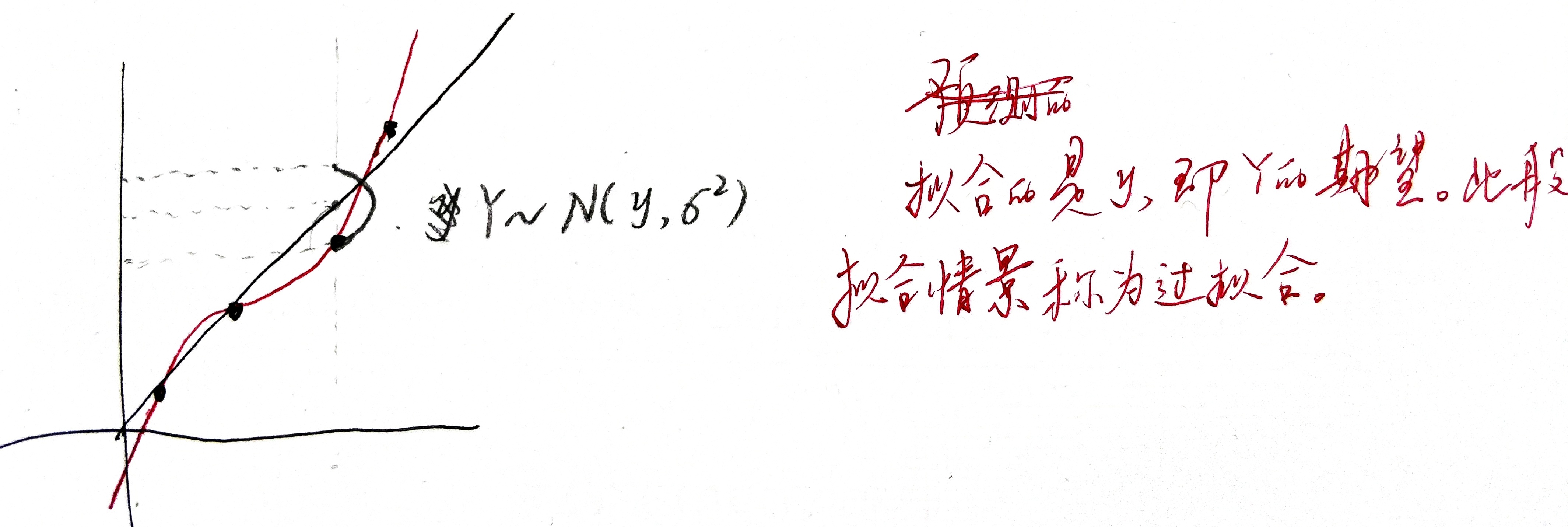
而当用最大似然来做模式识别时， $\mu$ 是未知的，极大似然是用 $\overline{Y}$ 来估计 $\mu$ 的，此时拟合出的估计分布的方差自然为 $\frac{1}{n}\sum (Y_i-\overline{Y}{)}^2$ ，对于无偏估计 $\frac{1}{n}\sum (Y_i-\mu {)}^2$ 来说，当且仅当 $\mu =\frac{1}{n}\sum Y_i$ 时取得最小值，故在数据量过少，而模型复杂度很高的情况下，用极大似然做拟合时（极大似然倾向于将拟合出的估计分布的方差做到最小），为使方差足够小，会导致 $\overline{Y}$ 与 $\mu$ 偏差过大，称之为过拟合，即过拟合的现象是 $\overline{Y}$ 与 $\mu$ 偏差过大，本质是参数自由度过高导致的方差过小 。

计算

对 $p(t|x;w,\beta )$ 建模，通过最大化样本的出现概率（直接拟合）求解模型参数，没有先后验一说。

似然函数为： $$p(y|x;w,\beta )=\prod _i^{N}N(f(x_i,w),\frac{1}{\beta })=\prod _i^N(\frac{\beta }{2\pi }{)}^{\frac{1}{2}}{e}^{-\frac{\beta }{2}(f(x_i,w)-y_i{)}^2}$$ 对数似然为： $$\ln p(y|x;w,\beta )=-\frac{\beta }{2}\sum _i^N(f(x_i,w)-y_i{)}^2+\frac{N}{2}(\ln \beta -\ln 2\pi )$$ 可在对数似然的极值处求得 $w_{ML}$ ，进而得到 $\frac{1}{{\beta }_{ML}}=\frac{1}{N}\sum _i^N(f(x_i,w_{ML})-y_i{)}^2$ 。

最终得到拟合的估计分布为 $p(y|x;w_{ML},{\beta }_{ML})=N(f(x_i,w_{ML}),\frac{1}{{\beta }_{ML}})$ 。

贝叶斯估计（最大后验估计）

计算

对 $p(t|x;w,\beta )$ 建模，通过最大化参数的后验概率求解模型参数。

由 $$p(w|x,y;\alpha ,\beta )\propto p(y|x;w,\beta )p(w|\alpha ),$$ 设先验概率为（其中 $\alpha$ 为超参数，为模型参数的先验方差的倒数） $$p(w|\alpha )=N(0,{\alpha }^{-1}I)=(\frac{\alpha }{2\pi }{)}^{\frac{M+1}{2}}{e}^{-\frac{\alpha }{2}{w}^{T}w},$$ 故后验概率为 $$(\prod _i^N(\frac{\beta }{2\pi }{)}^{\frac{1}{2}}{e}^{-\frac{\beta }{2}(f(x_i,w)-y_i{)}^2})(\frac{\alpha }{2\pi }{)}^{\frac{M+1}{2}}{e}^{-\frac{\alpha }{2}{w}^{T}w}$$ 取对数得 $$\sum _i^{N}p(y_i|x_i;w,\beta )+\frac{M+1}{2}(\ln \alpha -\ln 2\pi )-\frac{\alpha }{2}{w}^{T}w$$

故最大化后验概率等价于最小化该函数 $$\sum _i^N(f(x_i;w)-y_i{)}^2+\frac{\alpha }{2}{w}^{T}w.$$ 故先验即为正则项。

贝叶斯推理

MLE、MAP是选择相对最好的一个模型（point estimation）， 贝叶斯方法则是通过观测数据来估计后验分布(posterior distribution)，并通过后验分布做群体决策，所以后者的目标并不是在去选择某一个最好的模型，贝叶斯估计复杂度大，通常用MCMC等近似算法来近似，这样做模型的ensemble的优点是它可以reduce variance。

总结

首先建立数据的参数模型$p(D;w)$，通过带参模型计算各样本出现的概率，然后

• 最大化所有样本出现的概率，求得模型参数。（MLE）$\underset{w}{max}p(D|w)$
• 将在所有样本$D$已知的条件下模型参数$w$的概率称为模型的后验概率，最大化模型的后验概率，求得模型参数。（MAP）$\underset{w}{max}p(w|D)=\underset{w}{max}p(D|w)p(w)$
• 求出模型的后验概率分布$p(w|D)$，用积分做群体决策$\int p(y|x;w)p(w|D)\mathrm{d}w$。（贝叶斯推理）