卷积神经网络适用场景:输入信号在空间上和时间上存在一定关联性的场景。
封面图左侧为基础网络结构的调整,右侧为基础网络深度的增加。
一次卷积的计算量(FLOPs)为\(O(k*k*C_{in}*M*N*C_{out})\),一次卷积的参数量(MAC)为\(O(k*k*C_{in}*C_{out})\)。其中卷积后的大小为\(M=\frac{M-k+2*padding}{stride}+1\);若希望卷积前后大小一致,则需设\(padding=\frac{k-1}{2}\)且\(stride=1\)。
\[ (f*g)(n) = \int_{-\infin}^{+\infin}f(x)g(n-x) \mathrm{d} x \]
两个在某种角度上具有一定关联性的函数 f 与 g,在二者自变量之和为一常数 n 的约束(更一般化地,在二者自变量的线性组合为一常数的约束)下,两函数之积在某个区间上的积分称为这两个函数在该区间上的卷积。
总之,两函数的卷积是两函数之积在某种线性组合(如 x+y=n)的约束下的特殊积分。
之所以称为卷积,是因为该运算的结果是两函数的张量积构成的平面(或超平面)沿两函数各自自变量线性组合等式约束的轨迹做卷褶得到的降维的线(或超平面)上的某一点(线性组合等式约束决定的点)的值。
简而言之就是将张量积卷褶后的重合点之和即为卷积。
从对单通道二维图像做卷积的角度理解:
f 为图像像素值对位置的函数,g 为实现某种功能的滤波器(又称为卷积核、模板),其具体操作为对两矩阵的哈达玛积的所有元素求和。
要想实现更加复杂的非线性滤波器,需要用一大堆的简易非线性滤波器,并通过很多层的组合得到。NIN(network in network)提出了一种“偷吃步”的方法(MLPconv)来降低计算复杂度和模型复杂度。可从两个角度来理解 MLPconv:
(假设第一层的卷积核与输入图像相同大小)
从结构形式的角度:\(k_1\) 个卷积核输出到 \(k_1\) 个神经元上,再假设第二层的卷积核与第一层神经元数大小相同,\(k_2\) 个卷积核输出到 \(k_2\) 个神经元上,即对\(k_1\)种线性滤波的非线性激活结果再次进行\(k_2\)种线性滤波,依此继续连接;能够由此实现任意一种非线性滤波器的原因与传统神经网络能够模拟任意函数的原理一样。
故 MLPconv 本质为一个传统的神经网络(理解本质时用),即将一个传统的神经网络作为卷积核,神经网络隐藏神经元数由卷积核数决定,即希望得到的非线性滤波器个数。
由此,可将线性滤波器看作 MLPconv 的特殊情况,即一个感知机。
从物理含义的角度:\(k_1\) 个卷积核输出\(k_1\)个特征图(此处每个图仅为一个点),而第二层的每个感知机是对\(k_1\)个通道的特征图的同一个位置作线性组合操作,然后做非线性激活,该操作可理解为对\(k_1\)个通道的特征图的同一个位置做 1×1 大小卷积核的卷积,或者理解为对\(k_1\)级联的特征图做 1×1 大小卷积核的池化(理解为池化,是目的导向的,因为此操作的目的是对不同特征进行不同方向的聚合;其与池化不同,因为参数都是要学习的,而非固定的);能够由此实现任意一种非线性滤波器的原因是不同特征的不同方向的多次聚合能够得到一种任意一种非线性特征。
故 MLPconv 等价于一个 k×k 卷积层后缀数个 1×1 卷积层(思考网络结构及实际编码时用)。
其中 1×1 卷积层也有人称之为跨通道参数的级联池化(cccp),实现跨通道的信息整合。
1×1 卷积层的意义主要在于线性组合,并作非线性激活;想当于做了一次非线性组合。
简单来说,非 NIN 结构的多层卷积是跨越了不同尺寸的感受野,在相同范围内的感受野只有一次简易非线性滤波;而 NIN 结构的多层卷积是作用在同一尺寸上的感受野,可认为在相同范围内的感受野由一次复杂的非线性滤波,能够提取更强的非线性特征。
针对不同尺度特征自然需要不同大小的卷积核,考虑到不同尺度特征可能属于同一级别的抽象,故提出了 inception 结构。该结构本质是对几个不同大小卷积核的 MLPconv 的结果的 concat。该结构的合理性是基于以下两点原因的:
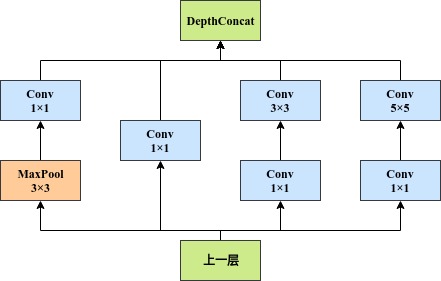
inception-v1 结构如下图所示(从左至右,为提取尺度越来越大的特征,最左侧的特征可认为是在该抽象程度上尺度为零的特征):

对 inception module 如此设计的理解:
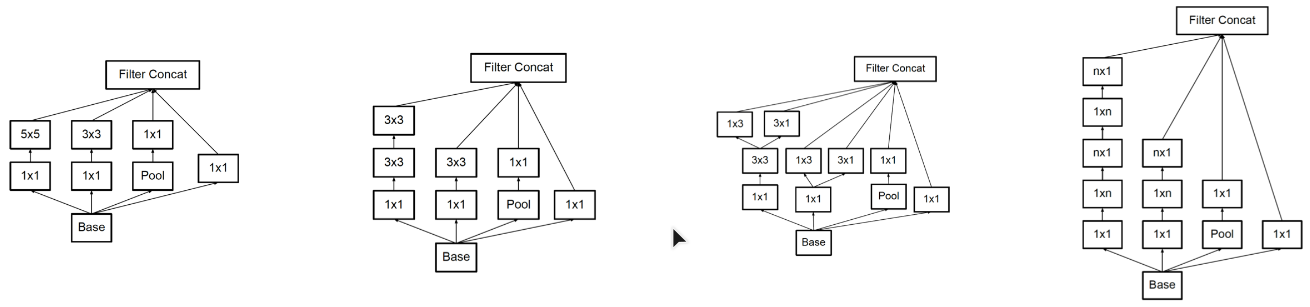
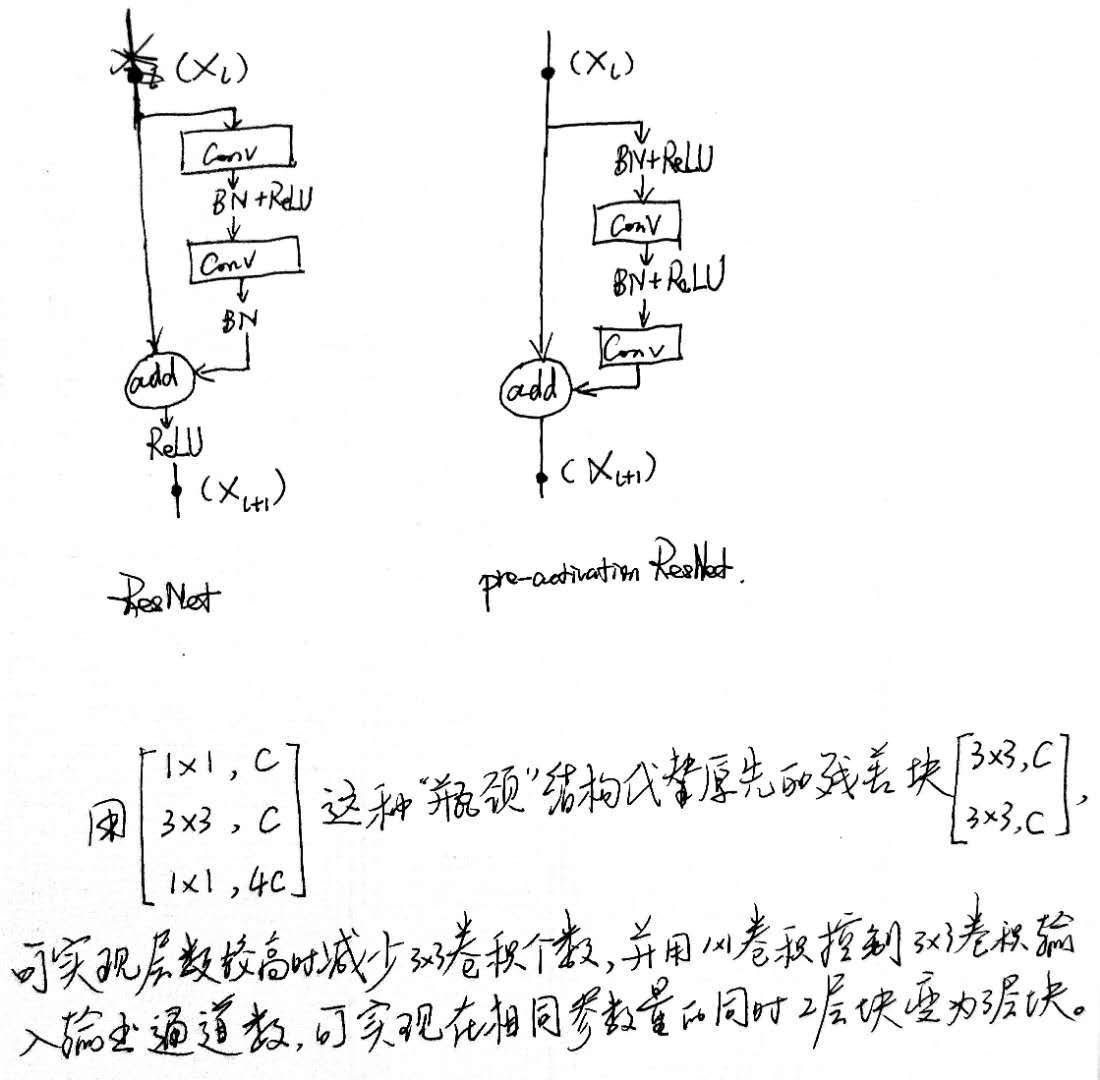
池化过程本质为特征突出过程,去除特征图中的无用像素点。(查看西瓜书的样本不均衡问题)

https://www.zhihu.com/question/59031444/answer/177786603
LRN层,对局部神经元的活动创建竞争机制,使得其中响应比较大的值变得相对更大,并抑制其他反馈较小的神经元,增强了模型的泛化能力。
很少再用,现多用 dropout。
- 一种更恶化环境训练、更舒服环境战斗的思想。
- Hinton 认为 dropout 是通过特殊的训练策略实现的隐式的模型集成。
简而言之:Dropout在实践中能很好工作是因为其在训练阶段阻止了神经元的共适应。
ResNet 是一种学习残差的框架,即用非线性层去显式地拟合一个残差映射,而不再是去拟合一个期望的潜在映射。
解决了随着网络层数不断加深,求解器不能找到解决途径的问题。
深度神经网络在 ReLU 和 BN 层的加入后,网络变深不再有梯度弥散的问题, 但却会出现随着网络的加深,准确度反而下降的现象,即退化现象。
ResNet 使得下述所需的函数变得更易拟合求解得到:通过几个非线性映射的堆叠去拟合一个恒等映射,由此使得对某个低级特征贡献不大的输入可以一下子被拉到更深的层,其对更高级特征的贡献由更深层的权重学习到。至于输入对哪种抽象特征的贡献度更大,在求解最优化的过程中可自动学习到。
从集成学习的观点,可以将更深的网络看做是在增加该指数的幂次( ResNet ),将更宽的网络看做是在增加该指数的基底( ResNeXt )。

卷积神经网络中的梯度反传是 2D,与传统神经网络中的 1D 反传不同,但其数学本质相同(见梯度反传),只是表现形式上有略微的不同:

池化层不需要计算梯度,因为没有要训练的参数,但在梯度反传时,误差的形状需要发生变化以保证和上一层的参数能够对位,处理方式的原则是:保证传递的误差总和不变:
对 CNN 的研究主要有三种方法: