
参考:https://blog.csdn.net/qq_35644234/article/details/57083107
图按照边的有无方向分为无向图和有向图。
图按照边或弧的多少分为稀疏图和稠密图,是个相对概念,只有在对比时才有其意义,可以用全局聚类系数来量化对比。下面的类型是绝对概念:
图上的边或弧带有权,则称为网(Network)。
如果有两个图 \(G = (V, E)\),\(G' = (V', E')\),满足\(V' \subseteq V\),\(E' \subseteq E\),那么,称\(G'\)是\(G\)的子图。
对于无向图,如果满足图中任意两个节点都存在路径(路径中间存在其他节点,也称为存在路径),则称为连通图(Connected Graph)。
无向图中的极大连通子图称为该无向图的联通分量(Giant Component),满足以下几点:
在数学理论中,图中的节点均为统一编号,不会存在不同的节点有相同编号的情况,也就是说若矩阵的行列索引为同一个值,即代表同一个节点,即简单图的邻接矩阵的对角线上的值均为0。接下来叙述的先从数学理论的角度进行。
设G的邻接矩阵为A,度矩阵为D(对角阵),那么拉普拉斯矩阵为:L = D - A。计算示例如下,显然,L是一个对称阵,是一个半正定阵。

L为什么要如此定义,其含义是什么呢?
在欧式空间中,将二阶微分算子(梯度的散度)称为拉普拉斯算子,即: \[ \Delta f = \nabla^2 f = \nabla \cdot \nabla f = \frac{\delta^2 f}{\delta x^2} + \frac{\delta^2 f}{\delta y^2} \] 将其从连续改为离散的二维矩阵表格,则拉普拉斯算子计算公式将变为: \[ \begin{align*} \Delta f &= \frac{\delta^2 f}{\delta x^2} + \frac{\delta^2 f}{\delta y^2} \\ &= f(x+1,y)-f(x,y)+f(x-1,y)-f(x,y)+f(x,y+1)-f(x,y)+f(x,y-1)-f(x,y) \\ &= f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)-4f(x,y) \end{align*} \] 将f(x,y)看为在矩阵(x,y)这个点的位置上的值,那么离散系统的拉普拉斯算子含义为,点(x,y)在各个方向上的梯度之和(称之为该点梯度的净流入)。
这里可以再解释一下细节,如上所述,离散系统的拉普拉斯算子在点(x,y)的值,是这个点周围的值变化(梯度)的总和,而一般习惯上定义函数值从小变到大即为梯度的正方向,即梯度值为正数,故,若算子的值为正数,则意味着在点(x,y)周围的值整体是要变大的,若算子的值为负数,则意味着在点(x,y)周围的值整体是要变小的。考虑到正梯度意味着变大,负梯度意味着变小,故将该算子的值称为梯度的净流入,更符合人类的直觉感觉(想像成山丘)。『净』是指非某一个方向,而是所有方向。故,重新叙述则为:梯度的净流入值越大(正得越大),周围的值整体将变得更大(高),梯度的净流入值越小(负得越大),周围的值整体将变得更小(低)。综上,拉普拉斯算子在某一点的本质为该点梯度的净流入。
这也是图像中拉普拉斯卷积核定义的由来: \[ \begin{bmatrix} 0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0 \end{bmatrix} \] 拉普拉斯卷积核一般用来做图像的边缘检测,变化后的图即为,梯度净流入的绝对值卡一个阈值后得到的图(轮廓图)。
将拉普拉斯算子推广到图数据结构上。设图G的节点全集为V,节点i的邻接节点全集为\(N_i\),节点i的度为\(d_i\),节点i的值为\(f_i\),节点i与节点j之间的边的权重为\(w_{ij}\)(\(w_{ij}=0\)表示节点i与节点j不相邻),那么在节点i的拉普拉斯算子为: \[ \begin{align*} \Delta f_i &= \sum_{j \in N_i} f_j - f_i \\ &= \sum_{j \in V} w_{ij} (f_j - f_i) \\ &= \sum_{j \in V} w_{ij}f_j - \sum_{j \in V} w_{ij}f_i \\ &= \sum_{j \in V} w_{ij}f_j - d_i f_i \end{align*} \] 即,将邻接节点的值全加起来后,减去(该节点的度*该节点的值)。这与上面描述的二维矩阵表格的算法本质上没什么不同,只是数学表示不同而已。将所有节点按编号排序,在所有节点上的拉普拉斯算子结果为: $$ \[\begin{align*} \begin{bmatrix} \Delta f_1 \\ \cdots \\ \Delta f_n \end{bmatrix} &= \begin{bmatrix} \sum_{j \in V} w_{1j}f_j - d_1 f_1 \\ \cdots \\ \sum_{j \in V} w_{nj}f_j - d_n f_n \end{bmatrix} \\ &= \begin{bmatrix} w_{11} & \cdots & w_{1n} \\ \cdots & \cdots & \cdots \\ w_{n1} & \cdots & w_{nn} \end{bmatrix} \begin{bmatrix} f_1 \\ \cdots \\ f_n \end{bmatrix} - \begin{bmatrix} d_1 & \cdots & 0 \\ \cdots & \cdots & \cdots \\ 0 & \cdots & d_n \end{bmatrix} \begin{bmatrix} f_1 \\ \cdots \\ f_n \end{bmatrix} \\ &= (A - D)f \\ &= -(D - A)f \\ &= -Lf \end{align*}\] $$ 故,拉普拉斯矩阵去左乘节点值构成的列向量,即为各节点的梯度净流出(因为有个负号)。
对于拉普拉斯矩阵,更为常用的是下面两种。
对称正则化的拉普拉斯矩阵,其定义为: \[ \begin{align*} L^{sym} &= D^{-1/2}LD^{-1/2} \\ &= D^{-1/2}(D-A)D^{-1/2} \\ &= D^{-1/2}DD^{-1/2} - D^{-1/2}AD^{-1/2} \\ &= I - D^{-1/2}AD^{-1/2} \\ &= \begin{cases} 1 & \text{i=j and } d_i \ne 0, \\ -\frac{1}{\sqrt{d_i d_j}} & \text{i ≠ j and } w_{ij} \ne 0, \\ 0 & \text{otherwise.} \end{cases} \end{align*} \]
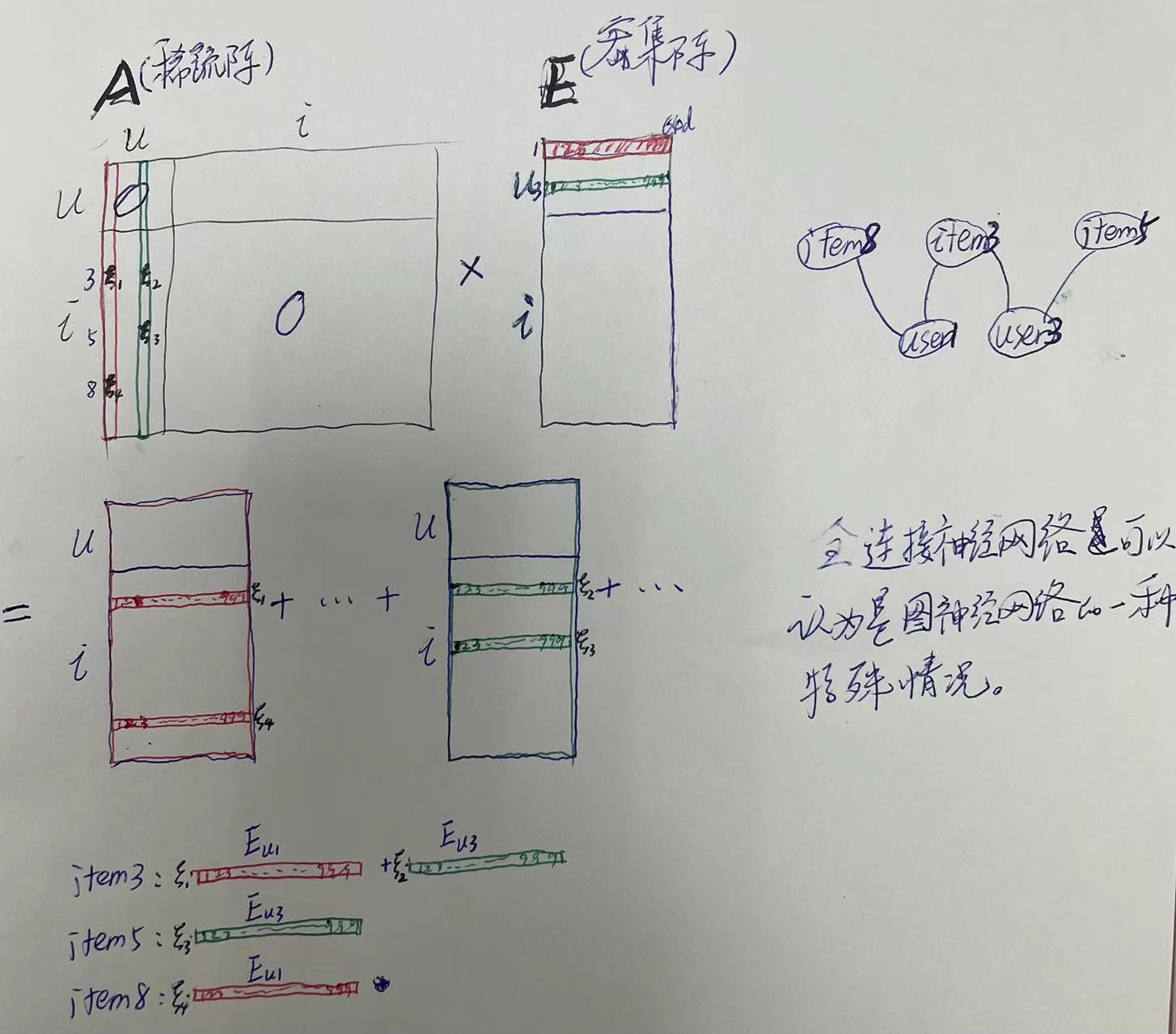
在工程实现上,为方便数值计算,一般将不同类型的节点分别编号,如编号为0的节点即可以是user类型也可以是item类型。常用的是一种非对称的边关系矩阵\(R\),若将行索引记为user类型的节点编号,列索引记为item类型的节点编号,那么第i行j列的值意为\(user_i\)和\(item_j\)节点之间的边关系。
基于\(R\),在表征邻接矩阵\(A\)时,便将某一类型的节点编号加上一个偏移量(另一个节点类型的最大编号值)。继续上述示例,若对item类型的节点编号加偏移量,那么邻接矩阵\(A\)表示为: \[ \begin{bmatrix} 0 & R \\ R^T & 0 \end{bmatrix} \] 接下来的对称正则化拉普拉斯矩阵计算便与数学理论上的方法一般无二了。
在工程上,除\(L^{sym}\)外,其中的\(D^{-1/2}AD^{-1/2}\)部分也很常用,常称为正则化的邻接矩阵,本文将其记为\(A^{norm}\)。 \[ A^{norm} = \begin{cases} \frac{1}{\sqrt{d_i d_j}} & \text{i ≠ j and } w_{ij} \ne 0, \\ 0 & \text{otherwise.} \end{cases} \] 正则化的邻接矩阵\(A^{norm}\)左乘节点向量矩阵含义:
随机游走正则化的拉普拉斯矩阵,其定义为: \[ L^{rw} = D^{-1}L = I - D^{-1}A \] 即,把对角线上的度用1代替,其他表示边的-1,用该行所属的节点的度的-1 次方的相反数代替。可能在传播、流行学习任务中比较有用。
TODO:谱聚类(拿拉普拉斯矩阵做特征分解)(看完这里,可能对拉普拉斯矩阵会有更深入的理解)
邻接矩阵的表示方式用两个数组来表示图的信息,一个一维数组表示每个数据元素的信息,一个二维数组(邻接矩阵)表示图中的边或者弧的信息。
优点:
缺点:
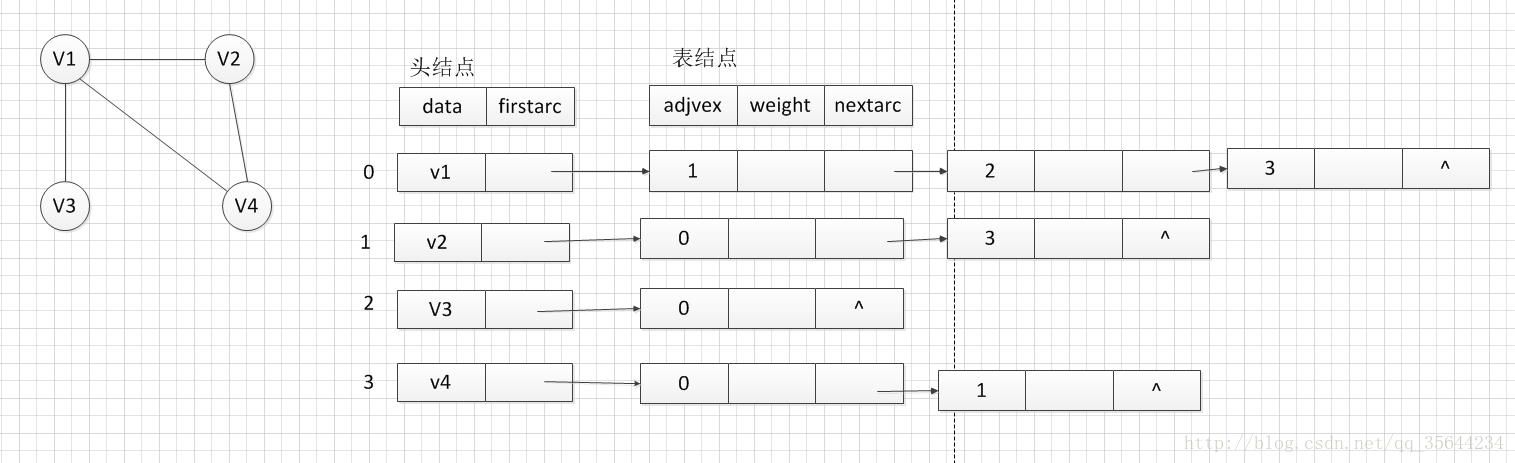
将数组和链表结合。主要是应对邻接矩阵在顶点多边少的时候,空间浪费的问题。
节点通过一个头结点类型的一维数组来保存,每个节点的所有邻接点组成一个链表后缀在其头结点上。
具体来说,其中每个头结点的firstarc都是指向一条依附在该节点的边的信息(表结点),表结点的adjvex表示该边的另外一个节点在一维数组中的下标,weight用于存储边的权重,nextarc指向的是下一条依附在该节点的边的信息。
优点:
缺点:
有向图的一个专有的链表结构,用于解决节点入度计算难的问题。
从图中某一个顶点出发遍访图的其余所有顶点,且使所有顶点被访问且只访问一次。这个过程,就叫做图的遍历(Traversing Graph)。
把构造连通网的最小代价生成树称为最小生成树(Minimum Cost Spanning Tree)。
非网图的最短路径,是指两顶点之间经过的边数最少的路径。网图的最短路径,是指两顶点之间经过的边上的权值之和最小的路径。路径上的第一个源点,最后一个顶点是终点。


