Doing

https://hrl.boyuai.com/chapter/intro

https://karpathy.github.io/2016/05/31/rl/

基础

Q-learning

用一个表格（Q表）记录在不同状态下采取各个动作所能得到的潜在回报。

这一算法的关键是学习的目标设置：将『采取该行动后得到的奖励 + 采取动作后的新状态下的最大Q值（无论将来再采用哪种动作）』作为在原状态下实施对应行动后的Q值的目标值，即，\(r_{s\_new} + \gamma Q_{s\_new}\)。

• 第二项为什么要用『采取动作后的新状态下的最大Q值』：
  • 本质是模型使用方式决定的。因为模型在最终使用时，输出的动作就是对应Q值最大的。从最终状态往前倒推，实施的即为一串Q值最大的动作序列，为保证模型从任一状态开始都能最大概率地导向最优状态，设计某一状态下任一动作的Q值时，便需要将后续大概率采取的一系列动作也考虑进来。

Q表更新（学习）规则： \[ Q_{s_0, a_0} = Q_{s_0, a_0} + \alpha [(r_{s_1} + \gamma Q_{s_1}) - Q_{s_0, a_0}] \] 其中 \(\gamma\) 为未来奖励的衰减率，\(\alpha\) 为学习率，对其做递归展开得（设 \(\alpha = 1\) ）： \[ \begin{align*} Q_{s_0, a_0} &= Q_{s_0} \\ &= r_{s_1} + \gamma Q_{s_1} \\ &= r_{s_1} + \gamma (r_{s_2} + \gamma Q_{s_2}) \\ &= r_{s_1} + \gamma r_{s_2} + \gamma^2 r_{s_3} + \dotso \end{align*} \]

故 \(\gamma\) 越大，对未来考虑越多。

详见demo(treasure_on_right) 。

Deep Q-learning（DQN）

用神经网络来实现Q表的功能，解决状态取值为连续值的问题。

将采取动作后的回报值作为DNN预估值，相当于多个目标的回归任务，目标个数即为全部的动作个数。

训练细节：

• fixed Q-targets：可以理解为右边的网络是左边的镜像，但只在每 200 个 batch 后才做 target_replace_op（将左边的网络参数更新进右边的网络中），避免label分布变化频繁，从而保证稳定收敛。通常称右边的网络为target_model，左边的网络为online_model。
• 经验回放：每 5 步做一次学习，大前提是已做了至少 200 步的仿真（记忆库最大容量设为 2000，每个 batch 是从记忆库中随机挑选的）
  • 使样本满足独立假设（非独立同分布的数据对训练神经网络有很大的影响，会使神经网络拟合到最近训练的数据上，即容易出现某种维度上的过拟合，导致泛化性变差）。在 MDP 中交互采样得到的数据本身不满足独立假设，因为这一时刻的状态和上一时刻的状态有关，采用经验回放可以打破样本之间的相关性，让其满足独立假设。
  • 提高样本效率。每一个样本可以被使用多次。
• epsilon-贪婪策略、玻尔兹曼策略：TODO

详见demo(DQN/run) 。

Double DQN

理论上来说，DQN的设计会天然存在Q值高估问题：本质是DQN设计的label计算逻辑导致的正向误差累积。

可以从任一状态开始往前倒推来理解。假设在某一状态下采取任一动作后的Q值均为0（或者相差无几），若target_model在某一动作上存在微弱高估，执行max操作后，\(r_{s\_new} + \gamma Q_{s\_new}\) 即为偏高的label，online_model可能会估得偏低可能会偏高，估得偏低时不会出现什么特别的影响，而一旦估得比偏高的label更高时，执行target_replace_op后，target_model也会估得更高；状态往前推，因为通过max操作选label，高估的信息便会继续往前传递，逐渐累加。对于动作空间较大的任务，DQN 中的过高估计问题会非常严重，造成 DQN 无法有效工作的后果。

实际表现会是什么样子：TODO（模型输出的Q值出现大于预设分布最大值的情况？这又怎么影响实际应用的有效性的呢？）

Double DQN的解决方案：在计算label时，max操作和Q值操作不用同一个网络（target_model），而分别用两个网络（max用online_model，Q值用target_model），从而缓解正向误差累积问题。

Prioritized Replay DQN

Dueling DQN

有很多任务，在部分场景中，Q值只受当前状态影响，无论采取什么动作，期望回报区别不大。比如避障任务中没有障碍的场景，承接条数识别任务中承接与否无所谓的用户。

模型预估两部分，价值函数V（不考虑动作，可以理解为预估的是在某一状态下采取任一动作后Q值的均值），和优势函数A（预估的是在某一状态下采取该动作后的Q值 相较于 采取任一动作后Q值 的优势）（若样本为动作a1，该样本是否更新其它动作对应的优势函数部分？）。即将原目标 \[ Q^{online\_model}_{s} = r_{s\_new} + \gamma \max{Q^{target\_model}_{s\_new}} \] 中的Q值计算改为两个输出值的计算： $$ Q^{online_model}{s} = V^{online_model}{s} + A^{online_model}_{s} \

Q^{target_model}{s_new} = V^{target_model}{s_new} + A^{target_model}{s_new} \[ 对于建模不唯一性的问题（对于同样的Q值，如果将V值加上任意大小的常数C，再将所有A值减去C，则得到的Q值依然不变，这会导致训练的不稳定性），通过在计算Q值时再减去一项优势函数的最大值，从而调整最优动作的优势函数值为0，由此确保V值建模的唯一性=max(Q)（TODO 有待理解。。。）： \] Q^{online_model}{s} = V^{online_model}{s} + (A^{online_model}{s} - ) \

Q^{target_model}{s_new} = V^{target_model}{s_new} + (A^{target_model}_{s_new} - ) $$

另外，通过用两个目标的方式来去学习也可以解建模不唯一性的问题（待尝试）。

价值函数： \[ V^{online\_model}_{s} = td\_target \] 和优势函数： \[ A^{online\_model}_{s} = td\_target - V^{online\_model}_{s} \] 其中 $$ td_target = r_{s_new} + \

Q^{target_model}{s_new} = V^{target_model}{s_new} + A^{target_model}_{s_new} $$ 这里td_target依然采用max的方式去做，会不会有问题？

Policy Gradient

DQN 状态可以达到无限，但输出的是已设定的各个动作的Q值（潜在回报值），故动作数量依然是有限的（有几个输出神经元便是所能采取的动作数量）；通过直接输出动作的值而不是某个动作后的回报值的方法，可使得输出动作达到无限，这种方法称为 Policy Gradient。

通过奖励的设置，来去改变回传的梯度的大小（也可以理解为label的置信度），这也是叫PG的原因。

与DQN的本质区别：DQN学的是各个动作后的回报值，PG学的是下一个动作（动作取值 如移动的偏移值，或 动作id的概率）。即PG是在解分类问题，DQN是在解回归问题。（类比 PG在做时长满意分类，DQN在做观看时长回归？）

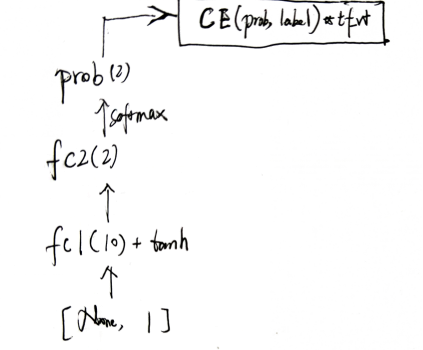
因为label是直接用的模型输出的action，所以为了避免每条样本的CE都是0，实际操作时选用label的action会引入随机。

与DQN更新的策略不同，DQN可以单步更新参数，而PG只能回合更新。因为虽然label引入了随机，但CE的期望值依然是0，只能用奖励修正loss的期望，故PG只能回合更新（若没完成回合，则所有的动作奖励都是0；除此之外，若即使有奖励值来去修正，但不是同一个回合的样本的话，也会因为随机抽取样本，样本分布发生变化(比如奖励低的资源异常地多)，导致效果变差）。

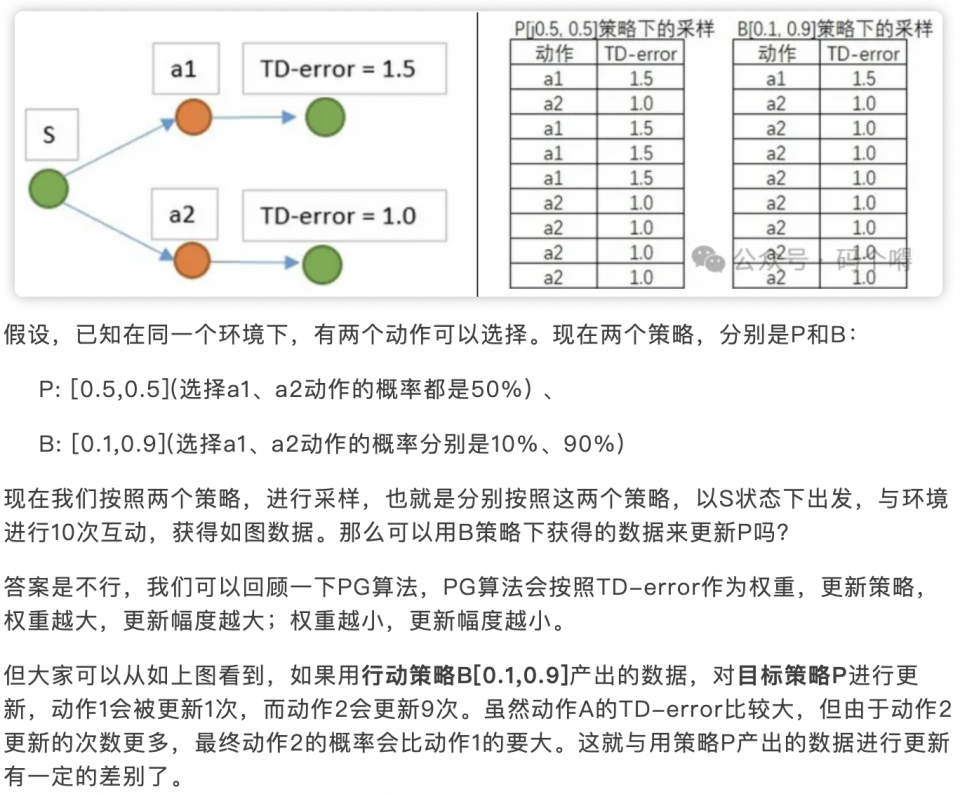
PG方差太大，lr正常设置容易无法收敛，lr往小里设置收敛太慢（PG为啥方差会很大？）

详见demo(RL_brain/demo) 。

Actor Critic

对PG中用于修正loss期望的奖励，用DQN来预估，这样就能解决PG只能回合更新的问题了。PG称为Actor，DQN称为Critic。

Critic的引入为什么能够减少PG的方差？

TRPO

PPO

PPO 利用 New Policy 和 Old Policy 的比例，限制了 New Policy 的更新幅度，让 Policy Gradient 对稍微大点的学习率不那么敏感。

PPO的关键就两点：

1. 通过重要性采样调整每个样本的权重（等价于调整action的分布），从而实现不依赖重新采样新数据的情况下进行策略更新；
2. 快模型输出截断，从而实现快模型的更新不偏离慢模型太多（等价于置信区域）；

标准PPO

以『倒立摆』为例。

训练流程：

• actor有两个模型，快慢模型，慢模型用来产出样本，快模型训练10个epoch后将参数更新到慢模型上。
• 每个epoch训练时，actor的loss在回传梯度时不更新critic部分。在快模型将参数更新到慢模型上后，critic模型再训练10个epoch。
• 每个epoch训练完后所有tensor的梯度都重置成None

样本收集：

• 由上次样本的next_state作为本次的state（若没有则随机初始化一个state），慢模型根据输入的state输出动作取值的分布(均值&方差)（常规的模型相当于只输出了均值），随机采样得到动作取值actionx。并根据env计算执行动作后的reward和next_state，由此产出一条样本：state, actionx, reward, next_state, done

critic

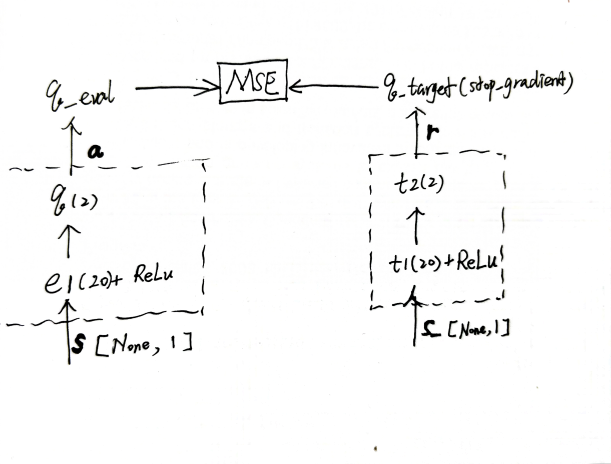
\[ loss = \text{MSE} (\text{CRITIC}(state), td\_target) \]

\[ 其中，td\_target = reward + 0.9 * \text{CRITIC}(next\_state) * (1 - done) \]

• td_target 是带衰减的累积奖励，其中reward是状态走到next_state上后的奖励
• critic模型只有状态值的输入，故可以认为critic预估的是 在输入状态下执行任一动作后获得的累积奖励的均值
• 『倒立摆』任务中，reward值域为(-1.0342, 1]

actor

\[ loss = -\min{[A * ratio, A * ratio|^{1.2}_{0.8}]} \]

\[ 其中，ratio = \frac{p_{actionx}}{p_{actionx}^{old}} \\ A = td\_delta + 0.9 * 0.9 * A_{next} \\ td\_delta = td\_target - \text{CRITIC}(state) \]

• loss的设计即为希望梯度回传让模型找到在状态state上时采取哪个actionx时能够最大化A
• 其中，A：
  • A已从计算图中分离，故可认为是常量，优化器只能通过改变ratio来降低loss，即通过改变ratio的分布来将所有样本的A*ratio的均值最大
    • 若优势函数为负值，则降低ratio，若优势函数为正值，则增大ratio；A的绝对值越大，降低/增大ratio的幅度便会越大
    • 因\(p_{actionx}^{old}\)为慢模型的输出值，也可认为是常量，故：
      • 优势函数为负值时，优化器将会降低\(p_{actionx}\)（mu远离actionx，增大std），越负降低的幅度越大；
      • 优势函数为正值时，优化器将会增大\(p_{actionx}\)（mu靠近actionx，减小std），越正增加的幅度越大；
  • td_delta为时序差分误差，含义为在状态state下执行动作actionx得到的累积奖励比执行任意动作高/低多少
  • 为简化逻辑，可先暂时不考虑优势函数的累积，则优势函数A即为时序差分误差
• 其中，ratio：
  • 计算ratio的p是actor模型输出的动作值为actionx时的概率
  • 在刚开始训练时，所有样本的ratio应该都几乎是1，但A是新的critic模型的预估值（按理应该更准），与慢模型的actor不是同一个，故随着训练的过程，ratio分布将会发生变化，使得所有样本的A*ratio的均值逐渐趋于最大。
  • 重要性采样：
    • 称ratio为重要性采样项，将慢模型的采样数据重新加权，匹配新策略，从而能够在不依赖重新采样新数据的情况下有效利用已有数据进行策略更新（即同份数据训练10个epoch）
    • 对于原始的policy-gradient该项为MSE(\(p_{actionx} - p_{actionx}^{old}\))，样本由慢模型产出，所有样本的优势值的分布是由慢模型采样出来的，因为采用mini-batch的方式更新模型参数，所以样本的分布会很影响模型收敛效果，即直接用慢模型的产出将会存在如下问题：

• 此外，A：
  • 优势函数的估计有两种方式，这里用的是时序差分法估计。另外还有蒙特卡洛法估计：
    • 蒙特卡洛方法通过对完整的轨迹进行采样，执行动作actionx后，用实际的回报来估计价值函数。即A = R(state, actionx) - CRITIC(state)，R(state, actionx)是采样的实际回报，也就是从执行动作actionx开始到一个完整回合结束后的累积reward。
    • 该方法缺点是方差较大，因为单次采样可能会受到偶然因素的影响，估计结果可能不稳定。
  • 时序差分法方差较小，因为它依赖于多个小步的估计，平滑了每一步的波动。但该方法由于使用了估计的价值来更新，可能会引入一些偏差。因此，两种估计方法的选择是在偏差和方差之间的权衡。
  • 由此引入广义优势估计，定义如下。当λ=1时，GAE退化为蒙特卡洛方法，方差较大但无偏；当 λ=0时，GAE退化为时序差分方法，偏差大但方差较小。

\[ A = reward + \gamma\text{CRITIC}(next\_state) - \text{CRITIC}(state) + \gamma * \lambda * A_{next} \]

判断离线模型有变好的指标：

• 相同动作次数的样本窗口下，reward（不是累积奖励）之和。

#### RLHF中的PPO

https://huggingface.co/blog/zh/the_n_implementation_details_of_rlhf_with_ppo

https://zhuanlan.zhihu.com/p/645225982

DDPG

为了继续用DQN的off-policy，且能应对连续action的任务。

相较于DQN主要有三个改动：

• 因为是连续action，没法比较多头的Q值，选最大action的Q值作为target；故采用state和action都为模型输入的DQN，并新增加一个在给定状态下输出能产生最大Q值的action的网络。
• 目标网络采用软更新的方式，而不是延迟更新的方式。
• 相较于DQN没有概率输出了，为了提高探索能力，引入随机噪声。

在目标检测中的应用

RPN

Deep Reinforcement Learning of Region Proposal Networks for Object Detection

详见 pdf ，source 。