分类错误的样本数占样本总数的比例。 \[ err = 1-acc \] ### 精度(acc)
分类正确的样本数占样本总数的比例，用于衡量分类器正确的识别新样本的能力。 \[ acc = (TP+TN)/(TP+TN+FP+FN) \]
衡量分类器不将负样本错误地识别为正样本的能力。 \[ P = TP / (TP+FP) \] ### 查全率、召回率(Recall)
衡量分类器查找所有正样本的能力。 \[ R = TP / (TP + FN) \] 对于多类别，模型的精度是指准确率的微平均(micro-avg)，模型的查准率是指准确率的宏平均(macro-avg)。若样本分布为自然分布，那么微平均衡量的是模型当下的表现；而宏平均衡量的是模型未来的表现（考虑到自然分布可能会发生变化），属于风险预估。宏平均指标相对微平均指标而言受小类别的影响更大。【ref】
但当正负样本不平衡时，准确率或召回率这一评价指标将会有很大缺陷。比如训练一个用于识别癌症的模型，混淆矩阵为：
| normal | cancer | |
|---|---|---|
| normal | 98 | 0 |
| cancer | 1 | 1 |
那么： \[ P_{cancer} = 1/(1+0) = 1, \\ R_{cancer} = 1/(1+1) = 0.5 \] ### F值
故，当正负样本均衡时既不能单独看查准率也不能单独地看查全率，由此引入F值： \[ F_{\alpha} = \frac{(\alpha^2 +1)PR}{\alpha^2 P + R}, \alpha > 0. \] \(\alpha\) 用于衡量查全率对查准率的相对重要性，\(\alpha > 1\) 更看重查全率，反之更看重查准率，标准的\(F_1\)意味查全查准重要性等同。故此时可用\(F_1\)这一评价指标来评价该模型对癌症这一类别的识别能力： \[ F1_{cancer} = 2 * (1 * 0.5)/(1+0.5) = 0.667 \]
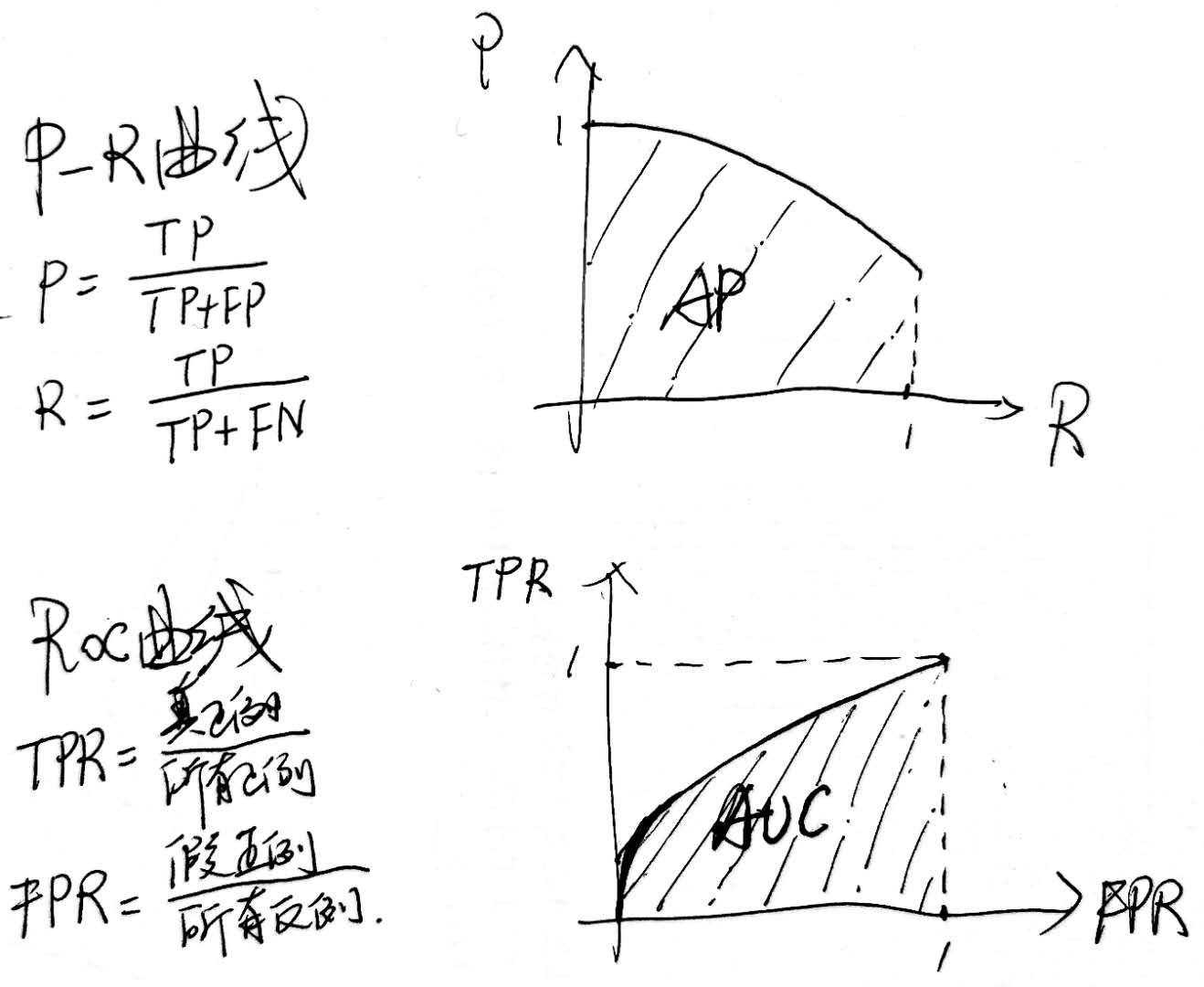
P-R曲线、ROC曲线定义如下：
P-R曲线下的面积为AP，即在不同召回率下准确率的均值，而mAP即为各类AP的平均。
ROC曲线下的面积为AUC（1-AUC也可作loss函数），计算方法如下：
上图算法3中，因为是排序后的，所以rank的值代表的是能够产生前大后小这样的组合的个数，通过只捞组合里第一个为正样本的情况，即可得到算法2中正样本score大于负样本的对，但是这里包含了（正，正）的情况，所以要减去这样的组（即排在它后面的正例的个数）。