阅读量 ,评论量
GCN
参考:https://www.zhihu.com/question/54504471/answer/332657604
全连接神经网络可以认为是图神经网络的一种特殊情况。将FNN中每一层输出看做一个节点的特征表示,FNN的前向计算,即为GCN的消息传递。如下所示:
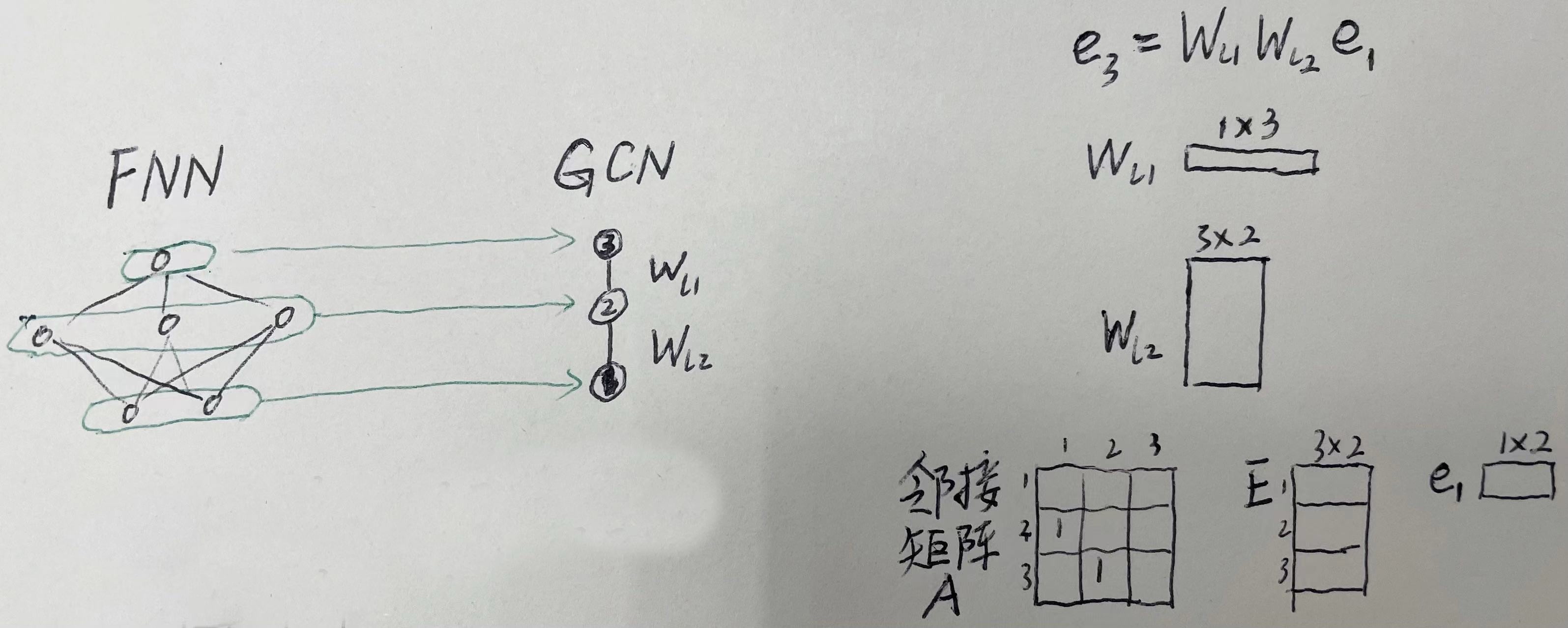
若FNN中有旁路的shortcut,那么A中每一行有值的列将不只一个。
GCN4Rec
NGCF
LGCN
相较于NGCF有两个变化:
1、消息传递:
- 舍弃特征变换和非线性激活:降低模型复杂度,提高模型收敛速度。从第K层传递过来的信息为:
\[
e_u^{(K)} = (A^{norm})^{K} E
\]
- 其中\(A^{norm}\)为正则化的邻接矩阵,左乘邻接矩阵可以表征信息传递的原理详见:图模型基础
- 当K=1时,拆解开的表示为:
\[
e_u^{(1)} = \sum_{i \in \{u的一阶邻接节点\}} \frac{1}{\sqrt{d_u d_i}}
e_i
\]
2、信息聚合
- 只用邻居节点传递过来的信息,不用节点的特征(即不采用自连接);聚合各阶邻居节点传递过来的信息时,对不同的层做加权和,从而达到与自连接相同的效果,以计算用户节点表征为例:
- 其中,k表示从第几层节点传递过来的信息,\(e_u^{(0)}\)表示该用户节点自身的emb(lookup来的那个),\(e_u^{(2)}\)表示第二层的节点向前传递两次后到该用户节点的信息。
\[
e_u = \sum_{k=0}^{K} \frac{1}{k+1} e_u^{(k)}
\]
- 对不同的层做加权和等价于自连接的原因如下:
- TODO:XXX推导证明(https://blog.csdn.net/weixin_44884854/article/details/108993222)
- 对不同的层做加权和的另一个角度的意义:不同层传递过来的信息具有不同的语义,以计算用户节点表征为例,第一层(k=1)对有交互行为的物品信息进行平滑处理,第二层(k=2)将在交互项上有重叠的用户信息进行平滑处理,诸如此般。更高层传递过来的信息能够捕捉更高阶的邻近性,但同时嵌入也会变得过平滑,简单地只使用最后一层会有问题(什么问题?),因此将各个层传递过来的信息结合起来一起使用,将使得用户表征更加全面。
- 过平滑问题:
- 过平滑的原因?做加权和就能解决?参考APPNP?(来自Personalized
PageRank的灵感)
socialLGN
在原交互图的基础上,引入一个社交图,交互图与社交图各自独立走LGCN的逻辑,只是在该次消息传递后的用户向量不仅仅只用从交互图上的LGCN中出来,而是用
交互图与社交图各自出来的用户向量做融合(item向量不变,依然从交互图上的LGCN中出来),然后再继续往后传递。如下所示:
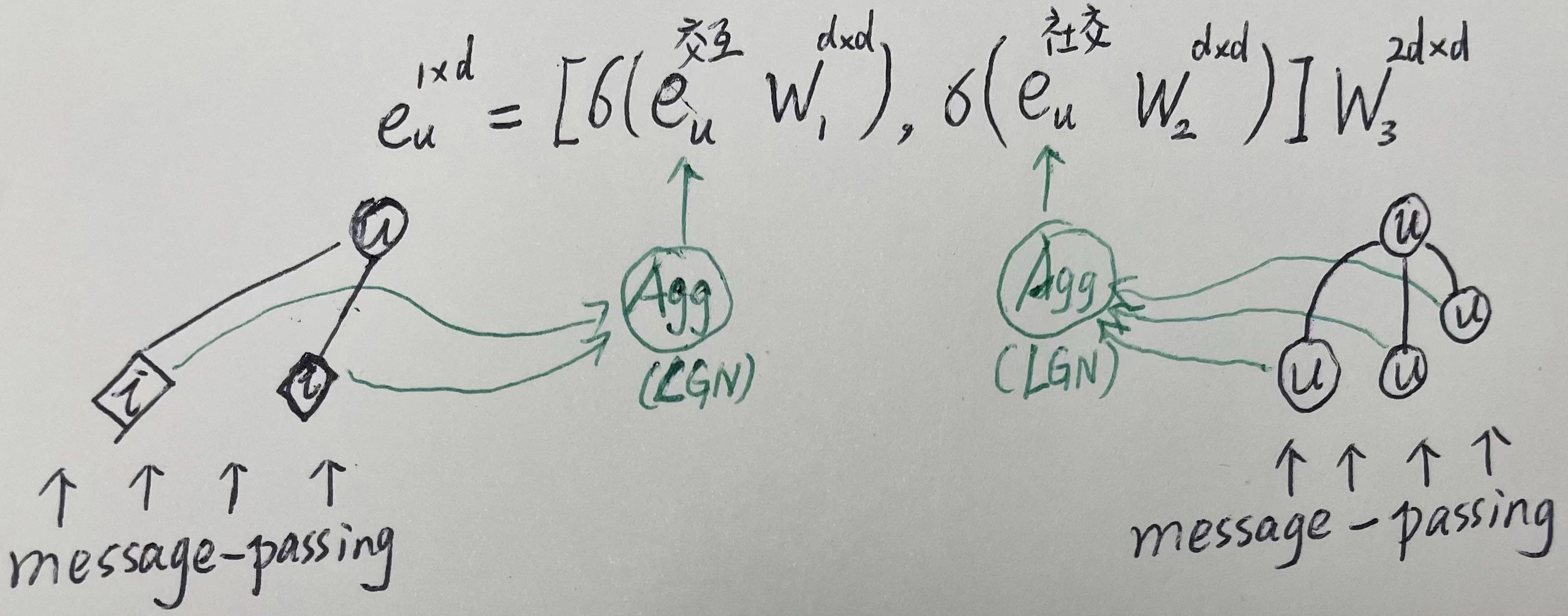
GraphSage
ErnieSage
GCN4Other


