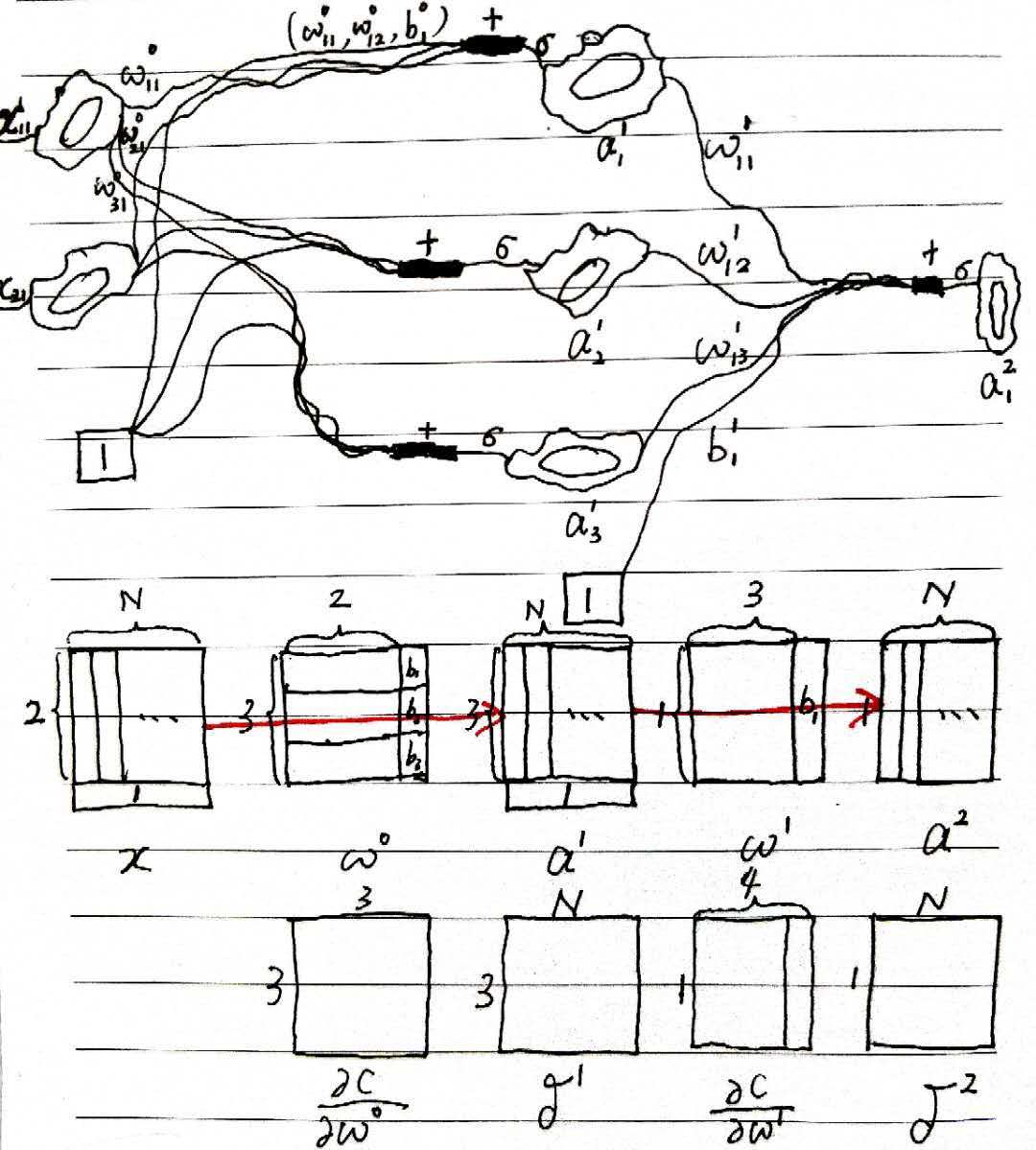
前馈神经网络一般有两种,linear perceptron network 和 RBF network,该文主要叙述前一种,其学习规则是梯度下降法,是一种无约束的最优化算法。

| 符号 | 含义 |
|---|---|
| \(L\) | 代价函数 / 损失函数 / 最优化目标函数 |
| \(w\) | “轴突”权重 |
| \(z\) | 第\(l\)层的带权输入 \(z^l=w^{l-1}a^{l-1}\) ,即从上个神经元轴突传到该神经元树突上的值 |
| \(\sigma\) | 神经元的激活函数 |
| \(a\) | 神经元的激活值 |
| \(\delta\) | 中间变量,称为某层的误差,专用于反向传播算法 |
注 1:零层为真实数据,无前传过程,自然没有所谓的误差 \(\delta^0\);因第零层的“轴突”上的权重 \(w^0\) 尚未学习成功而导致的第一层的神经元的带权输入 \(z^1\) 的误差,记为 \(\delta^1\) 。
注 2:每层“轴突”上的权重\(w\) 的行数为希望学到的模式数,列数为输入数据的维度。
注 3:做某一层的前传的时候,那一层的恒一神经元(用于模式中的偏置)才会被重新激活;当做为输出层时,该层的恒一神经元处于闭塞状态,是看不见的。当做某一层的反传的时候,是用该层神经元的误差\(\delta\) 求loss对上一层“轴突”权重的偏导,而该层的恒一神经元没有所谓的误差,上一层的恒一神经元却有“轴突”权重,自然也有偏导,故只有求“轴突”权重偏导的那一层的恒一神经元会被重新激活,其余均处于闭塞状态。
若 \(y\) 与 \((x_1,\dotsb,x_m)\) 线性相关,且采样没有噪声,则直接采\(m\)个样本点求解线性方程就能得到参数 \(\omega\) 的唯一解。为应对非线性相关的数据,采用迭代最优化(iterative optimization)的方法。
Ref:https://blog.csdn.net/heyongluoyao8/article/details/52478715
梯度是个向量,指函数变化增加最快的地方,故沿负梯度的方向便能到达函数的极小值处。
迭代优化的参数更新通式为: \[ w(t+1) \leftarrow w(t)+\alpha v(t) \quad , \alpha > 0 \] 其中参数的确定由降低 loss 函数的方法确定。对 loss 函数进行一阶泰勒展开: \[ L(w(t+1)) \approx L(w(t))+(w(t+1)-w(t))\nabla L(w(t)) \\ = L(w(t))+ \alpha v(t)^T \nabla L(w(t)) \] 要使 \(L(w(t+1))\) 最小,须使 $ v(t)^T L(w(t))$ 最小(因为前提假设loss是半正定函数),故令 \(v(t)= -\nabla L(w(t))\) 。为使得学习率在陡的地方大,缓的地方小,令 \(\alpha \propto ||\nabla L(w(t))||\) ,从而得到梯度下降法的参数更新式: \[ w(t+1) \leftarrow w(t)-\alpha_0 \nabla L(w(t)) \] 其中 \(\alpha_0\) 称为 fixed learning rate,而真实的 learning rate \(\alpha\) 的大小随梯度的大小变化而变化。
对 loss 函数进行二阶泰勒展开: \[ L(w(t+1)) \approx L(w(t))+(w(t+1)-w(t))\nabla L(w(t))+\frac{(w(t+1)-w(t))^2}{2}\nabla^2 L(w(t)) \\ = L(w(t))+F(w(t+1)-w(t)) \] 为使\(L(w(t+1))\)最小,令\(F(w(t+1)-w(t))\)达到负的最小即可,即置导数为零得: \[ \frac{\partial F(w(t+1))-w(t))}{\partial w(t+1))-w(t)} = 0 \\ => w(t+1))-w(t) = \frac{- \nabla L(w(t))}{\nabla^2 L(w(t))} \] 对应参数迭代更新通式,\(v(t)=\frac{- \nabla L(w(t))}{\nabla^2 L(w(t))}=-H^{-1}\nabla L(w(t))\),其中H称为海森矩阵,为函数的二阶偏导方阵,可用SVD求伪逆以保证数值稳定性。
海森矩阵计算费时,故有一些准牛顿算法来近似逼近,BFGS算法便是一种。BFGS算法通过迭代来逼近\(H^{-1}\) :
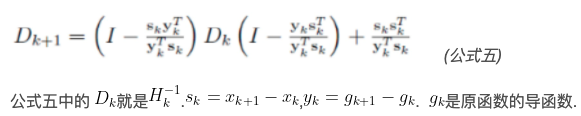
BFGS算法迭代过程中需要存储D矩阵,如果太大会导致可行性较差,可通过L-BFGS算法,以时间换空间的算法来节省内存。
与梯度优化算法沿着梯度最速下降的方向寻找函数最小值不同,坐标下降法依次沿着坐标轴的方向最小化目标函数值。
注意:
\[ \delta^l=(w^l\delta^{l+1})*\sigma'_{z^l} \\ \frac{\partial L}{\partial w^{l-1}}=\frac{1}{n}\delta^{l}(a^{l-1})^T \]
在用矩阵编程计算梯度时,无需考虑具体矩阵乘积的细节和含义,在得到反向传播的标量表达式后,只需依照两条规则即可写出梯度的矩阵算式:
\[ w(t+1) \leftarrow w(t)-\alpha_0 \nabla L(w(t)) \]
参数更新公式同GD,利用 Stochastic 的优势,以跳出局部最优点。
同步随机梯度下降法(Synchronous SGD)在优化的每轮迭代中,会等待所有的计算节点完成梯度计算,然后将每个工作节点上计算的随机梯度进行汇总、平均并上面的公式更新模型。之后,工作节点接收更新之后的模型,并进入下一轮迭代。由于Sync SGD要等待所有的计算节点完成梯度计算,因此好比木桶效应,Sync SGD的计算速度会被运算效率最低的工作节点所拖累。
异步随机梯度下降法(Asynchronous SGD)在每轮迭代中,每个工作节点在计算出随机梯度后直接更新到模型上,不再等待所有的计算节点完成梯度计算。因此,异步随机梯度下降法的迭代速度较快,也被广泛应用到深度神经网络的训练中。然而,Async SGD虽然快,但是用以更新模型的梯度是有延迟的,会对算法的精度带来影响。Async SGD的更新公式为: \[ w(t+\tau+1) \leftarrow w(t+\tau)-\alpha_0 \nabla L(w(t)) \] 对参数 \(w_{t+\tau}\) 更新时所使用的随机梯度是 \(\nabla L(w(t))\) ,相比SGD中应该使用的随机梯度 \(\nabla L(w(t+\tau))\) 产生了τ步的延迟。因而,我们称Async SGD中随机梯度为“延迟梯度”。
这种延迟梯度会影响模型收敛的准确性,并且这种现象随着机器数量的增加会越来越严重。
带延迟补偿的随机梯度下降法(ASGD with Delay Compensation)。ASGD中用的是 \(\nabla L(w(t))\) ,实际上应该用 \(\nabla L(w(t+\tau))\) ,那么能不能用 \(\nabla L(w(t))\) 来近似表示 \(\nabla L(w(t+\tau))\) 呢?将 \(\nabla L(w(t+\tau))\) 进行一阶泰勒展开: \[ \nabla L(w(t+\tau)) \approx \nabla L(w(t)) +(w(t+\tau)-w(t))\nabla^2 L(w(t)) \] 其中 \(w(t)\) 通过各work节点拉模型参数时缓存得到(即分work节点地保存模型参数,若共有5个节点,那么加上主版本的模型参数,ps应该共维护6份模型参数),主要难点就在于那个loss函数的二阶导了。根据费舍尔信息矩阵的定义,梯度的外积矩阵是Hessian矩阵的一个渐近无偏估计(点我看更多的推导细节),故: \[ \begin{align*} \nabla^2 L(w(t)) &\approx \nabla L(w(t)) \otimes (\nabla L(w(t)))^T \\ &\approx Diag(\lambda \nabla L(w(t)) \otimes (\nabla L(w(t)))^T) \\ &= \lambda \nabla L(w(t)) \odot \nabla L(w(t)) \end{align*} \] 由此代入SGD中: \[ \begin{align*} w(t+\tau+1) &\leftarrow w(t+\tau)-\alpha_0 \nabla L(w(t+\tau)) \\ &\approx w(t+\tau) - \alpha_0 (\nabla L(w(t)) +\lambda \nabla L(w(t)) \odot \nabla L(w(t))(w(t+\tau)-w(t))) \end{align*} \] 具体操作:各work节点在t步从ps中把模型参数w拉下来,并计算梯度 \(\nabla L(w(t))\) ,然后将节点编号和计算好的梯度推给ps,ps从缓存中拿到该节点对应的模型参数w(t),从主模型中拿到w(t+τ),计算得到w(t+τ+1),完成一轮更新。
参数服务器 + ASGD + AdaGrad 组成的优化算法。
更新公式为: \[ w(t+\tau+1) \leftarrow w(t+\tau)- \frac{\alpha_0}{\epsilon + \sqrt{\sum_{i=0}^{t}(\nabla L(w(i)))^2}} \nabla L(w(t)) \] 其中, \(\alpha_0\) 为预设的固定学习率,随着不断的迭代,学习率越来越小,梯度延迟的影响也会越来越小。
另外,实验发现,该优化算法的不一致性带来的随机性,对非凸问题求解很有效:
\[ \begin{align*} M(t) &= \alpha M(t-1) + (1-\alpha) \nabla L(w(t)) \\ w(t) &\leftarrow w(t-1) - \alpha_0 M(t) \end{align*} \]
通常,\(\alpha=0.9\),这意味着参数更新方向不仅由当前的梯度决定,也与此前累积的下降方向有关。这使得参数中那些梯度方向变化不大的维度可以加速更新,并减少梯度方向变化较大的维度上的更新幅度。由此产生了加速收敛和减小震荡的效果。
其本质为对梯度的滑动平均(指数加权平均,具体效果是一种时间衰减的效果),其原理如下:

注:
动量法能够减小高曲率方向上的震荡,使得小球尽快地损失掉重力势能。窃以为,公式结合物理原则,应为(尚未测试): \[ \begin{align*} v(t) &= \alpha M(t-1) - \epsilon (1 + \frac{1}{|\frac{\partial L}{\partial w}|}) \\ w &= w + v(t) \\ M(t) &= \frac{v(t)}{\alpha} \end{align*} \]
Ilya Sutskever 在2012年提出了一种优化版本:先在历史累计方向上前进一大步,然后在新位置上计算梯度并修正方向。可以这么理解,最好犯错之后去改正它。
【官方解释】
Adam,即 Adaptive Moment Estimation,对SGD-M的自适应预估。 \[ \begin{align*} g_t &= \nabla L(w(t)) \\ M(t) &\leftarrow \beta_1 M(t-1) + (1-\beta_1)g_t \\ \hat{M}(t) &\leftarrow \frac{M(t)}{1 - \beta_1^t} \\ v_t &\leftarrow \beta_2 v_{t-1} + (1-\beta_2)g_t^2 \\ \hat{v}_t &\leftarrow \frac{v_t}{1 - \beta_2^t} \\ w_t &\leftarrow w_{t-1} - \frac{\alpha_0}{\sqrt {\hat{v}_t} + \epsilon} \hat{M}(t) \end{align*} \] \(\hat{M}(t)\) 是对 \(E(g_t)\) 的估计,衡量了训练时关于更新梯度的信息;\(\hat{v}_t\) 是对 \(E(g_t^2)\) 的估计,即参数的方差估计,衡量了模型参数的稳定性。
定义 \(\frac{\hat{M}(t)}{\sqrt{\hat{v}_t}}\) 为信噪比,可以理解为,信噪比越高,意味着对当前梯度走向越有把握,从而得到更大的步长。
在迭代过程中,其中 \(\beta_1^2\) 和 \(\beta_2^2\) 会存在精度丢失的问题,可将公式做如下转换(以 \(\hat{v}_t\) 为例): \[ \begin{align*} g_t &= \nabla L(w(t)) \\ \hat{v}_t &\leftarrow \frac{v_t}{1 - \beta^t} \\ &\leftarrow \frac{\frac{v_t}{1 - \beta}}{\frac{1 - \beta^t}{1 - \beta}} \\ &\leftarrow \frac{\frac{\beta v_{t-1} + (1-\beta)g_t^2}{1 - \beta}}{\sum_{i=0}^{i=t}\beta^i} \end{align*} \] 故: \[ \begin{align*} d_t &\leftarrow \beta d_{t-1} + 1 \\ s_t &= \frac{v_t}{1 - \beta} \\ s_t &\leftarrow \beta \frac{v_{t-1}}{1-\beta} + g_t^2 \\ &\leftarrow \beta s_{t-1} + g_t^2 \\ \hat{v}_t &= \frac{s_t}{d_t} \\ \end{align*} \] 代入模型参数更新式中: \[ \begin{align*} d_t &\leftarrow \beta d_{t-1} + 1 \\ s_t &\leftarrow \beta s_{t-1} + g_t^2 \\ w_t &\leftarrow w_{t-1} - \frac{\alpha_0}{\sqrt {\hat{v}_t} + \epsilon} \hat{M}(t) \\ &\leftarrow w_{t-1} - \alpha_0 \hat{M}(t) \sqrt{\frac{1+\epsilon}{s_t/d_t +\epsilon}} \end{align*} \] 【另一种解释】
通过引入二阶动量放在学习率的分母上,来解决对于『经常更新但梯度不大』A 和『梯度接近于0不怎么更新』B,下一步A、B都有一个较大梯度回传时,B的更新量小于A的问题。相当于是 SGD-M 和 AdaGrad 两者的结合体 ,实现既能加速收敛(SGD-M)又能对稀疏的特征得到更大的更新。
对于经常更新的参数,我们已经积累了大量关于它的知识,不希望被单个样本影响太大,希望学习速率慢一些;对于偶尔更新的参数,我们了解的信息太少,希望能从每个偶然出现的样本身上多学一些,即学习速率大一些。所以我们需要一个东西去度量历史更新频率。考虑到对于梯度接近于0的参数自然不怎么更新,故我们可以用二阶动量来衡量滑动窗口内的历史更新频率。参数更新式如下: \[ \begin{align*} g_t &= \nabla L(w(t)) \\ M(t) &= \beta_1 M(t-1) + (1-\beta_1)g_t \\ v_t &= \beta_2 v_{t-1} + (1-\beta_2)g_t^2 \\ w_t &\leftarrow w_{t-1} - \frac{\alpha_0}{\sqrt v_t + \epsilon} M(t) \end{align*} \] 通常,\(\beta_1=0.9,\beta_2=0.999,\epsilon=10^{-8},\alpha_0=0.001\)。
由于Adam中的学习率主要是由二阶动量控制的,这就可能在训练后期引起学习率的震荡,导致模型无法收敛。通常解决方法为修改二阶动量更新公式,从而使得各参数的学习率都单调递减: \[ v_t = \max ( \beta_2 v_{t-1} + (1-\beta_2)g_t^2, v_{t-1}) \] 但进而又会引入另一个问题:后期Adam的学习率太低,影响了有效的收敛。故通常的方法为:前期用Adam,享受Adam快速收敛的优势;后期切换到SGD,慢慢寻找最优解。
其实某种算法是否有效,主要看你的数据是否符合该算法的胃口,算法固然美好,数据才是根本。
每个神经元入度的不同导致了流入不同神经元的“树突”权值的最佳学习率各不相同。当入度很大时,每个“树突”权值改变一点点,累积的改变量就很大了,很容易过量;而当入度很小时反之。所以一般采用一个全局学习率,然后根据对每个神经元各自做适当调整: \[ w+=-\epsilon g \frac{\partial L}{\partial w} \] 初始化局部 \(g=1\) ,如果下次该权值的梯度符号不变则增加 \(g+=0.05\) ,否则减小为 \(g*=0.95\) 。
注意:
- 将 \(g\) 限制在某个合理的范围,比如[0.1, 10] 或 [.01, 100]。
- 使用 full-batch 或很大的 mini-batch,毕竟这样保证了梯度的符号不易受 mini-batch 的采样误差影响。
- 综合自适应学习率和动量更新法,以当前梯度和当前速度的符号来决策 \(g\) 的变化。
全局学习率之所以难选,主要是因为每个期望的最终的权值的数量级相差巨大。在 full batch 中,可以利用梯度的符号来替代权值的更新量,从而解决这个问题。RProp结合了“只用符号”和“自适应学习率”的思想,但它违反了 SGD 的中心思想(当学习率很小的时候,权值更新量其实是当前mini-batch的梯度和历史梯度的平均。举例来讲,假设某个权值在9个批次中的梯度是+0.1,在第10个批次中的梯度是-0.9,我们希望这个权值大致不变。),故不适用于 mini-batch。而RMSProp便融合了mini-batch的高效性、mini-batch间的有效平均和RProp的稳定性。
对小数据集(10000以内)或者没有多少重复数据的大数据集,应当使用full-batch的一些优化方法,如Conjugate gradient、 LBFGS。然后试试adaptive learning rates, rprop …,它们是为神经网络而设计的方法。
对含有重复数据的大数据集,应当使用mini-batch。尝试动量法SGD,rmsprop 或LeCun的最新研究成果。
假设激活函数\(\sigma(z)=z\),则 \(L(\omega , b)=\frac{1}{n}\sum ||y- \{ \omega_{L-1}[\omega_{L-2}(...x)] \}||_2\),而我们平常所说的loss函数是与网络结构无关的“基础loss函数”。
\[ \sigma(z)=z \\ L=\frac{1}{2n}\sum_x||a(x)-y(x)||^2 \]
\[ \sigma(z)=\frac{1}{1+e^{-z}} \\ L=-\frac{1}{n}\sum_x[y\ln a+(1-y)\ln (1-a)] \]
用交叉熵而非均方差的原因是为了解决神经元饱和问题(指某些神经元可能因权重初始化不当或者确实已经学到了很成熟的地步,而处于 \(\sigma'(z)\) 值很小的激活值位置,进而导致在该处的梯度几近为零的现象;而其后果是神经元激活值会维持很长一段时间的近似稳定状态,这在训练终期是代表收敛的好现象,但若是在训练初期(即误差比较大时), loss 下降会十分缓慢,严重拖慢收敛速度):使用交叉熵会使得采用 sigmoid 激活的神经网络中的梯度表达式中的 \(\sigma'(z)\) 被约掉,从而解决了神经元饱和问题。
可根据激活函数和希望的梯度形式反推得到所需的loss函数,见神经网络与深度学习(Michael Nielsen)3.1.3节。
最小化交叉熵 loss 函数等价于最大化以 sigmod 为参数的对数似然,见数学_基础 信息论
\[ \sigma(z_i)=\frac{e^{z_i}}{\sum_ie^{z_i}} \\ L=-\frac{1}{n}\sum_x\ln a_I,(a_I为真实类别对应神经元的激活值) \]
- 因loss只求在真实类别神经元上的偏差,而激活函数的分母中所有神经元都包含,故\(\delta^L\)的求解分为两部分,求解过程如下: \[ \delta_i^L = - \frac{1}{a_I^L} \frac{\partial a_I^L}{\partial z_i^L} \\ a_I = \frac{e^{z_I}}{\sum_ie^{z_i}} \\ if \quad i \ne I: \frac{\partial a_I}{\partial z_i} = -a_ia_I, then \quad \delta_i^L = a_i; \\ if \quad i=I: \frac{\partial a_I}{\partial z_i} = a_I(1-a_I), then \quad \delta_i^L = a_I-1; \\ and, \quad y_i=\{^{0,i\ne I} _{1,i=I} \\ so, \quad \delta^L = a-y. \]
首先,要保证代码的 no bug,不仅指编译和运行时不会导致 core dump,还指神经网络可以确确实实地在拟合到一个可用的模型上,一般需要做如下工作:
然后开始做调参工作(测试集与训练集的loss最好同时保存,以便调参):
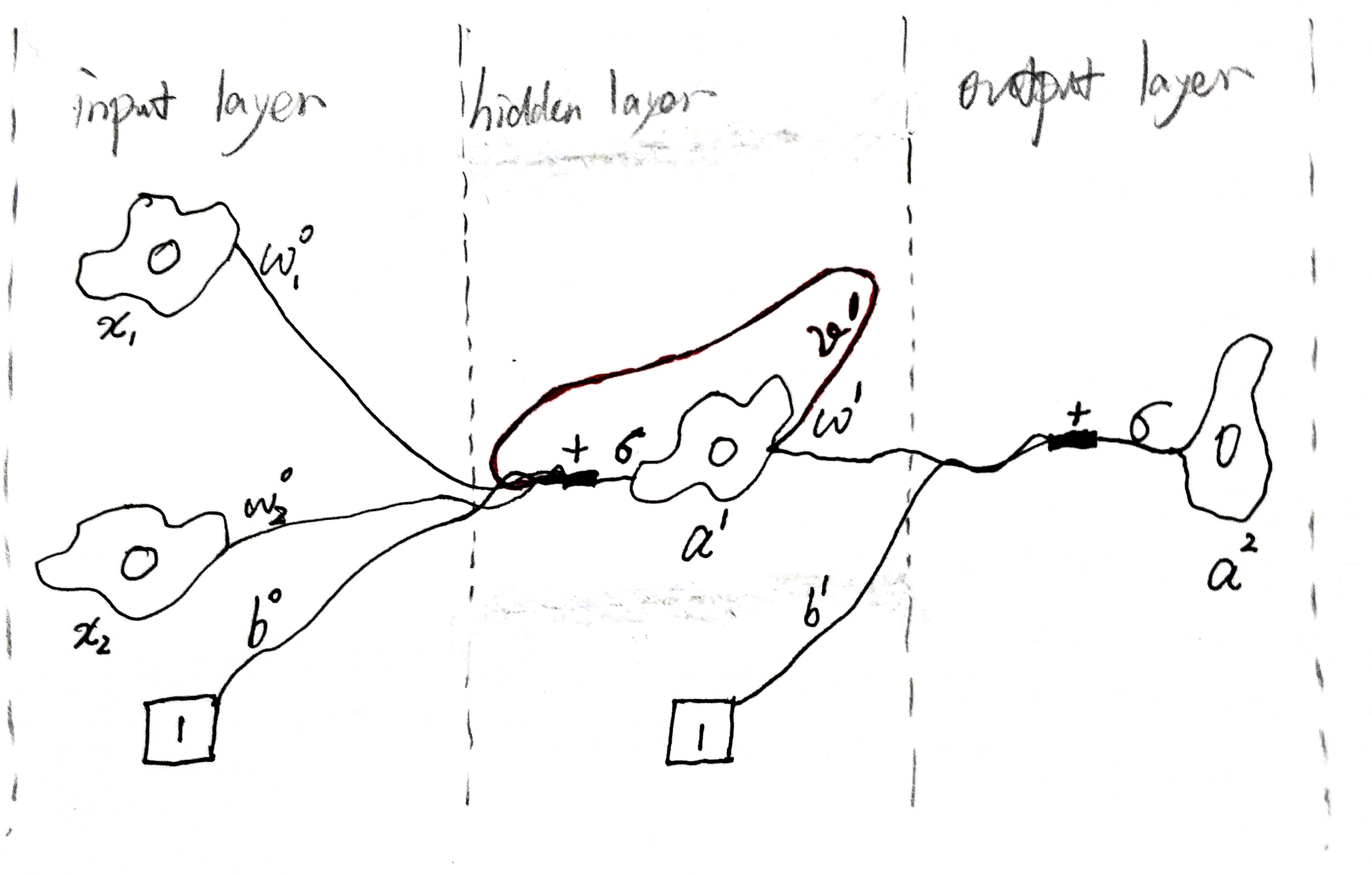
其中 \[ a^1 = \sigma(W^0 x + V^1 a^1). \]
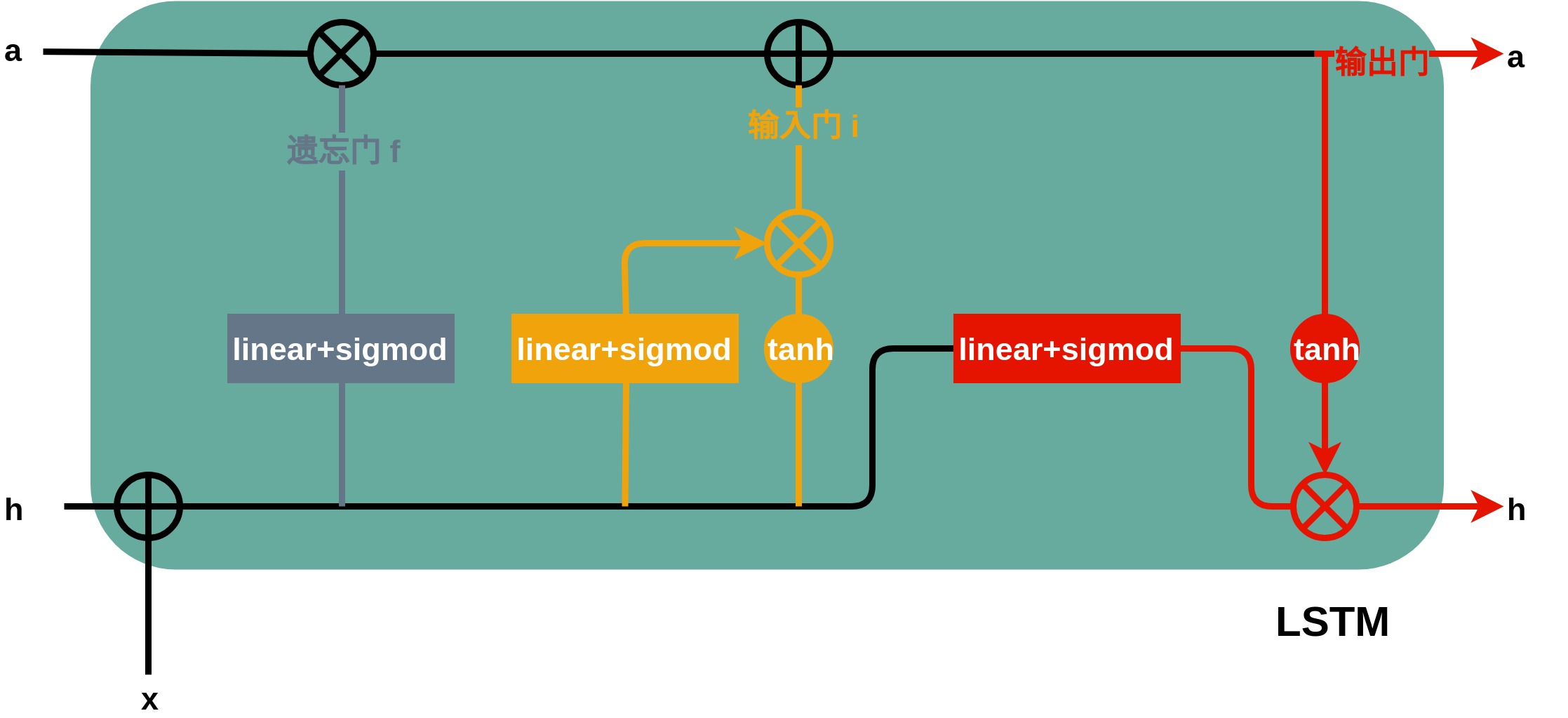
其中 \[ \begin{align} a_{t} &= f \odot a_{t-1} + i, \\ i &= \mathrm{linear\_sigmod} (h_{t-1} + x) \odot \mathrm{tanh} (h_{t-1} + x), \\ h_{t} &= \mathrm{linear\_sigmod} (h_{t-1} + x) \odot \mathrm{tanh} (a_{t}), \end{align} \] 即,遗忘门用于确定历史中的哪些信息需要保留,输入门用于确定当前输入中的哪些信息应当被添加进来,输出门用于更新该神经元的状态(包括激活值 a 和隐藏值 h )。